大二上学习笔记
目前是准备采用有比赛时打比赛总结
没比赛时看书学习理论的学习方法
顺带把书中的大部分实验也给整了
密码学
分组密码加密操作模式
ECB
电子密码本模式加密
简答来说就是分组加密,不足则补
大腿出的17届面试题acdes就是
ecb加密模式一个缺点就是密钥不变每次加密出来的密文都是不变的
这样就可以通过流量分析和代换攻击
还有个就是位图的加密
即使加密了还是能从图中读出信息
CBC
cbc密码分组链接模式
就是多了个iv
加密方法也有点改变
能使得每次加密出来的结果都不一样
加密方法是
第一个明文与iv xor后加密的y1
y1与第二个明文x2 xor
然后结果放去加密
然后再与下一次的明文xor
解密的话只需要多一步xor
如果每次加密都选择一个新iv这样每次的密文都会不一样
OFB
输出反馈模式
目前遇到的密码学就这些,其余很少遇到特别在逆向中
等遇到了再来填坑把
开启一波技术性学习
10/15
我来了
双重加密与中间人攻击
首先是密钥的不正确可能性
就是多解问题,比如用80位密钥加密分组宽度为64位明文
会出现2 64次方种密文
但是用的密钥有2 80次方个
所以会有多重映射关系
但是可以用多组明文密文对来测试可以大大减小错误密钥概率
还有就是双重加密之所以不安全是因为中间人攻击
理论上来说双重des加密如果通过暴力的话需要2 2k次方次测试密钥
但是中间人攻击可以使得复杂度变为单重des加密的倍数
主要实现就是先对明文一次加密打表
总共2 k次方
然后对密文解密然后比较查找 2 k次方
这样就是2 k+1次方次
所以说双重加密得不偿失
真正提升安全性还是三重加密
三重加密 and 密钥漂白
三重加密最典型的就是ede模式
加密解密加密
之所以这样是可以实现单词加密
对抗差分分析也十分有效
密钥漂白对密钥位数不足但本身以足够抵抗差分分析
才会有很好的效果
具体是xor
给明文xor后加密
xor后输出
//填坑
数学知识
把之前的数学知识补充一下把
感觉re进阶数学不能落下
逆向工程核心原理
windows消息钩取
一说到钩取肯定是和hook有关
消息钩取的实现简单来说就是
当键盘发生输入事件时,消息会被添加到OS message queue
然后根据判断哪个程序发生事件,再从OS message queue取出消息添加到application message queue
hook的钩链则存在于他们之间,先于application message queue看到消息。这样就能进行很多操作
如修改,阻止。
具体实现是 SetWindowsHookEx()函数
有个示例程序貌似不兼容win10,一开就崩
明天用虚拟机跑下试试
果然虚拟机可以了 win7x86
稍微逆向了下,看书上的源码还是有点懵逼的。。。
DLL注入
简介:对运行中的其他程序强行插入特定的dll文件
KCTF
达芬奇密码
正式开始接触看雪ctf
感觉和其他ctf的区别还是挺大的
特别是对于数学的要求
经常出现逆出解不出的状况。。。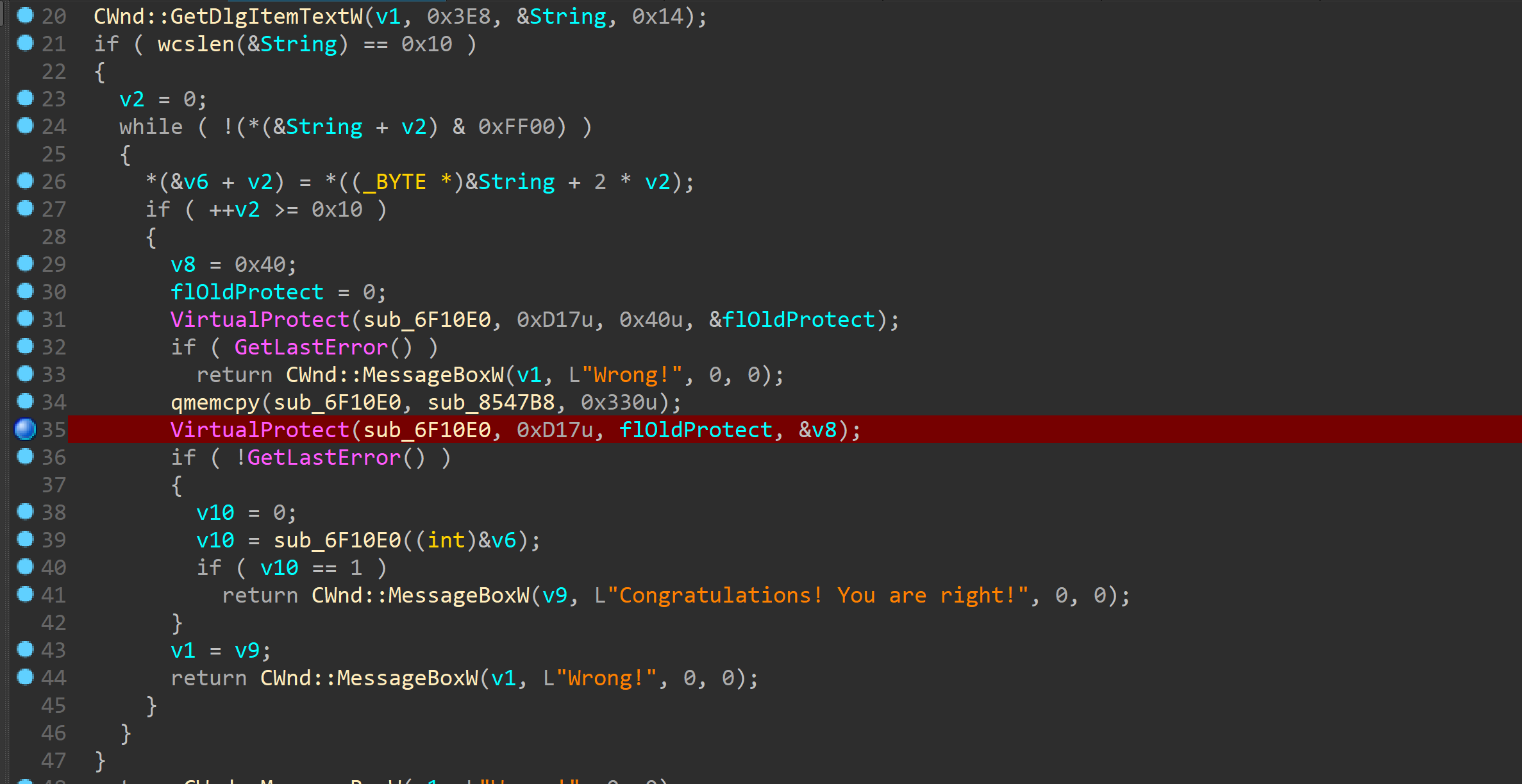
拖入ida后逻辑很简单,有个smc数据后memcpy
主要逻辑
首先是把输入与上面初始化的局部变量
逐个xor
然后开始平方
这边平方实现很奇葩看汇编看的
每个与最低位相乘后记录下值再与下一位加
连续循环8次
最后就是比较
就是x*2 - 7y**2 == 8
然后关键就是解方程了。。。
z3解不出。。。只好去学习一波sage
sage不能约束求解没办法
Mathematica
挺猛的
抽时间了解了解
最后写脚本就是多注意一个小端序问题
丛林的秘密
题目是个apk,解压后分析so库
可以发现在动态解密一个html文件
里面调用了wasm
机器码复制出来反编译成c
这边填了个坑
一开始是用
./wasm2c 1.wasm -o 1.c
然后反编译时疯狂报错
后来经室友一起查看
发现是因为名称不能以数字打头
他会修改一些神奇的宏定义
改成./wasm2c 1.wasm -o a.c即可
仔细分析发现逻辑并不复杂
1 | |
BYTECTF 2019
NaughtyBoy
apk逆向看了段时间
感觉不是一道太难的题目
来详细写下wp
//这边顺带夸一下不愧是r3得题,能学到好多
jeb里看不到什么,主要是看so库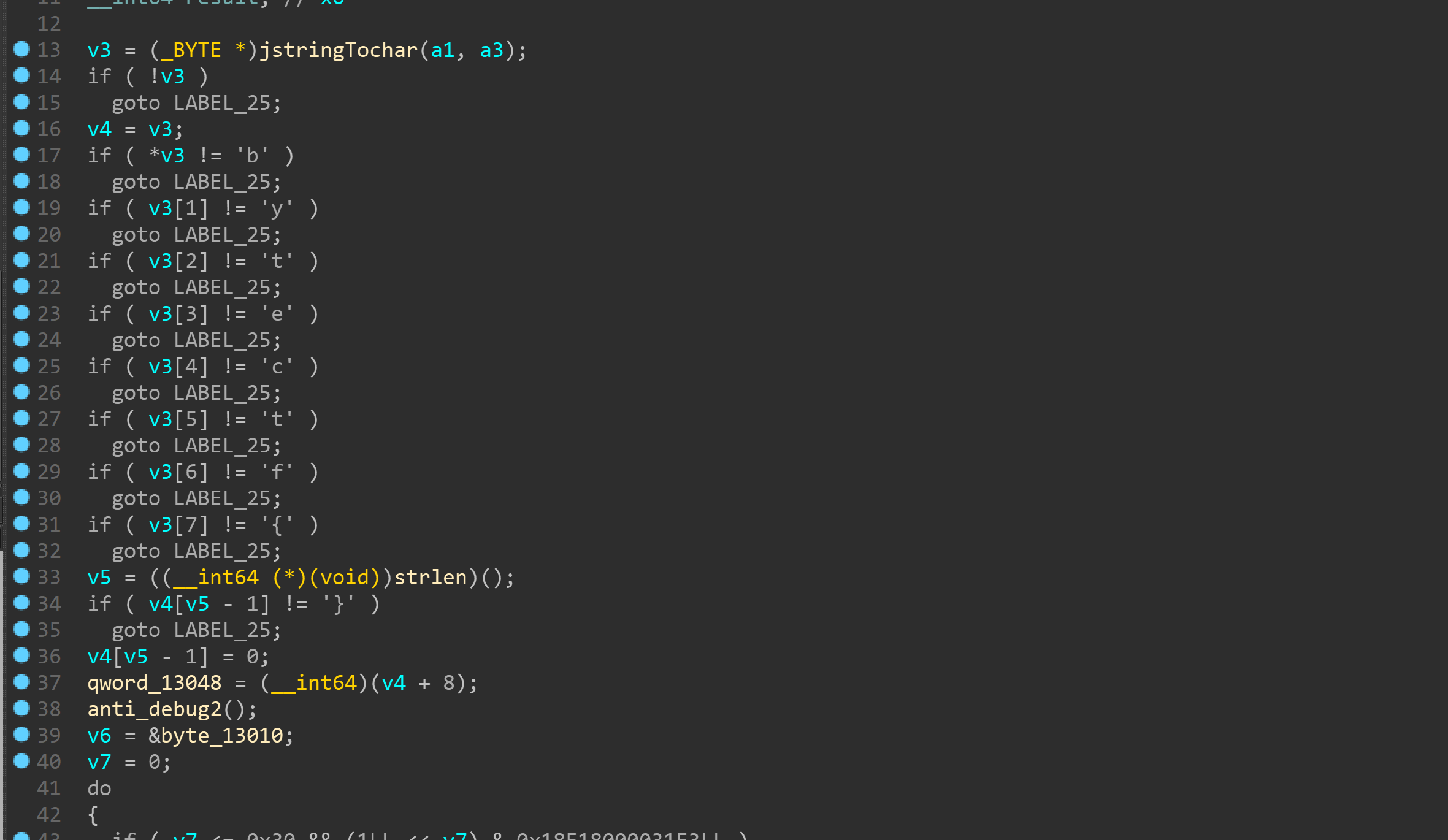
可以看到比较开头字符串和花括号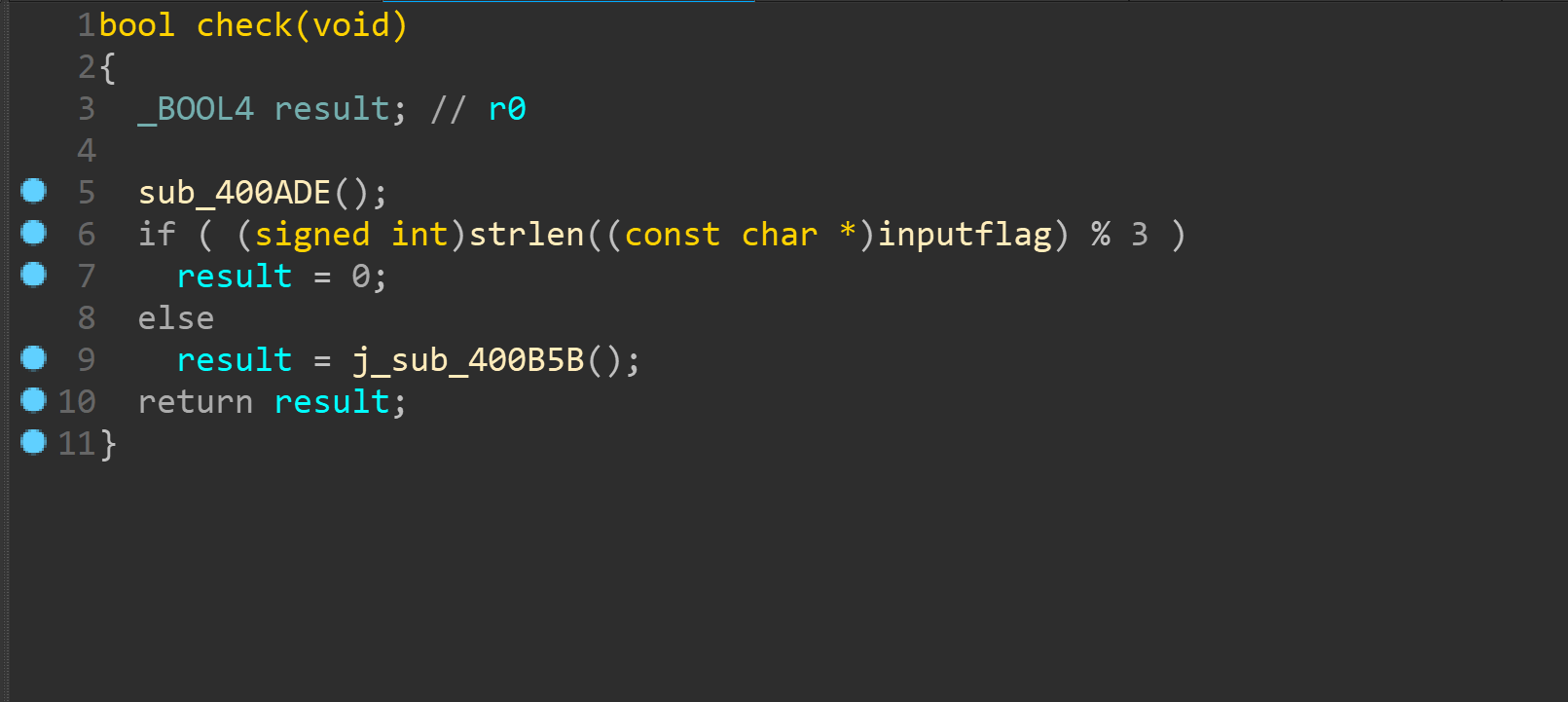
下面这个其实就是单纯得长度验证,要为3得倍数
然后进如check函数
进check之前还有一个sub_400ADE函数是初始化
首先是初始化地图,复制粘贴一下打出来即可
注意一下里面的antidebug2函数
初始化了全局变量byte_5004 = 0;
这在最后验证时有用
下面来看下check
一开始会对前四个字节进行解密操作
然后开始游戏
其实是一个变种的推箱子游戏
具体规则是每三个输入为一次
前俩个输入是坐标
会检查你当前的坐标是否是O
第三个输入是行为
这边为检查你行为的那边是否为O
比如你输入1往上走就检查你上面是否为O
然后你的位置与你上面的O被清空成路线,你上上方向变为O,类似推箱子
这样再看看地图可以推出来初始位置必须是5,3
且必须往上走
这样就可以进行爆破
1 | |
爆破出前四个为good
然后看下最终验证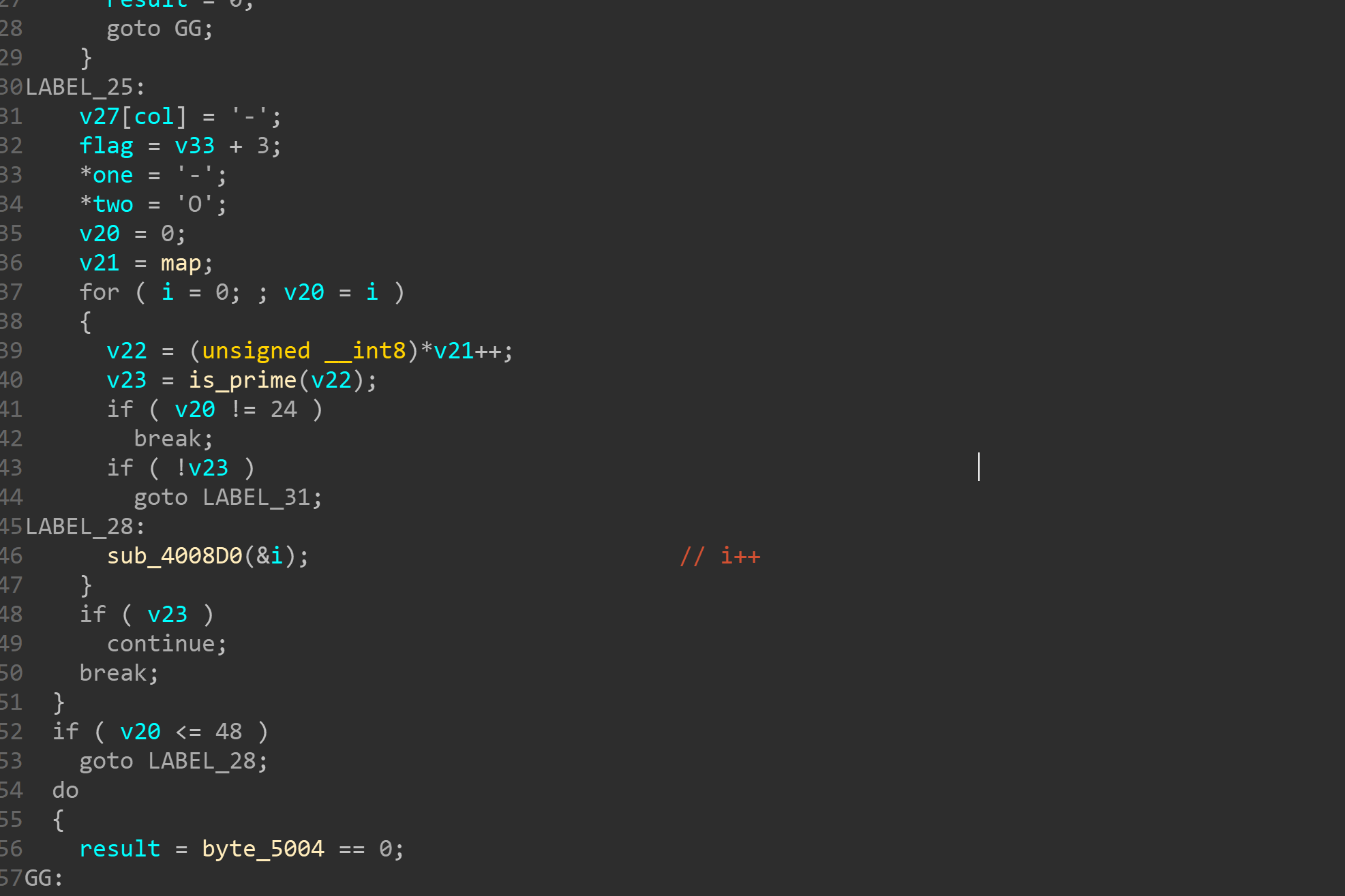
就是检查第24位是否为O
那很简单了照这样走下去就行
最终flag
bytectf{good53233212414531}
驱动逆向
驱动逆向写起来还是有点恐怖的。。。
踩了很多坑
首先最重要的就是调试
虚拟机配好环境后用windbg连
设置好entrypoint然后再虚拟机中加载sys驱动
windbg成功断下
改下参数后就可以解密了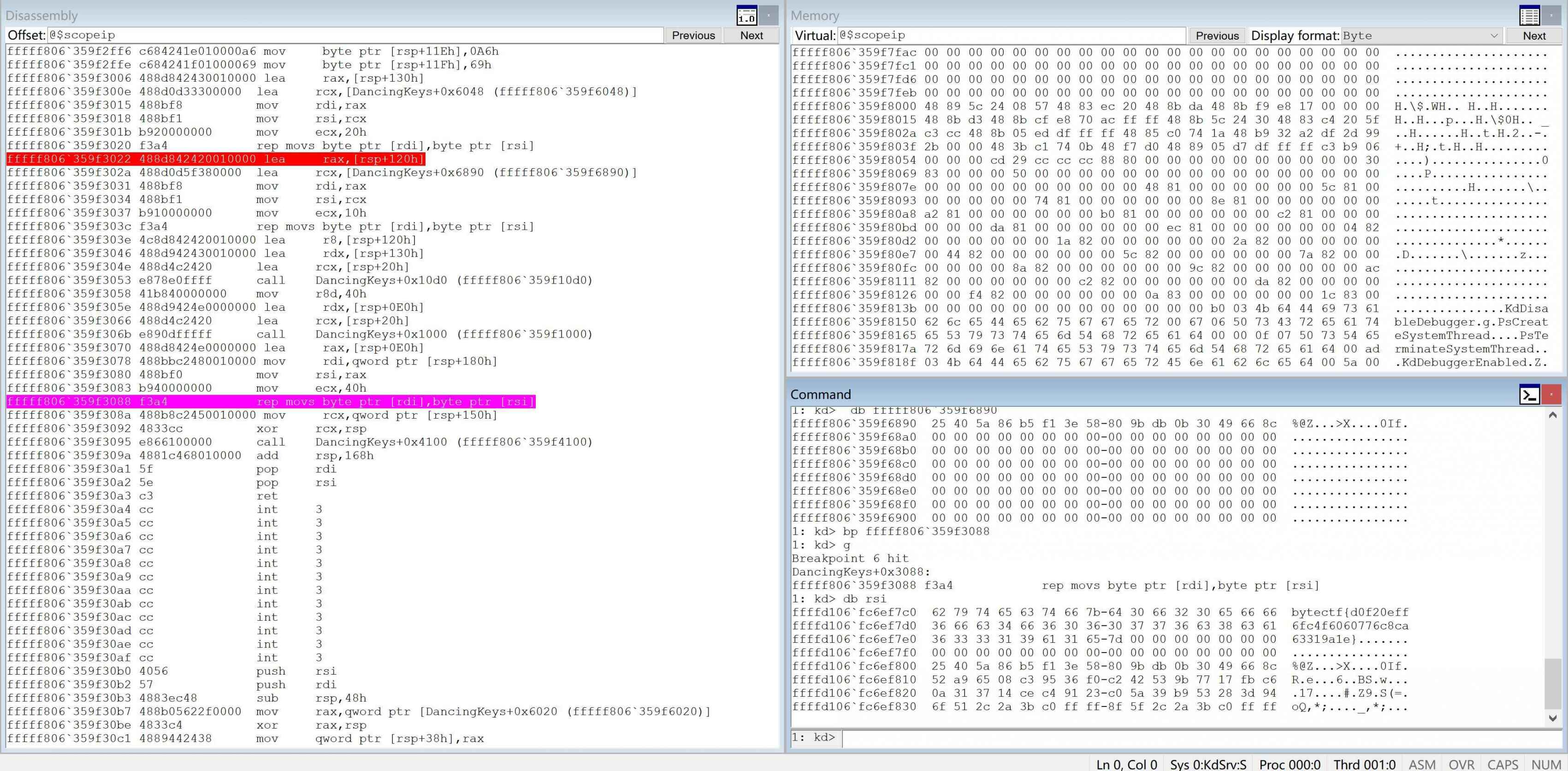
下面写下大致调试步骤
管理员运行windbg
File -> Kernel Debugging -> com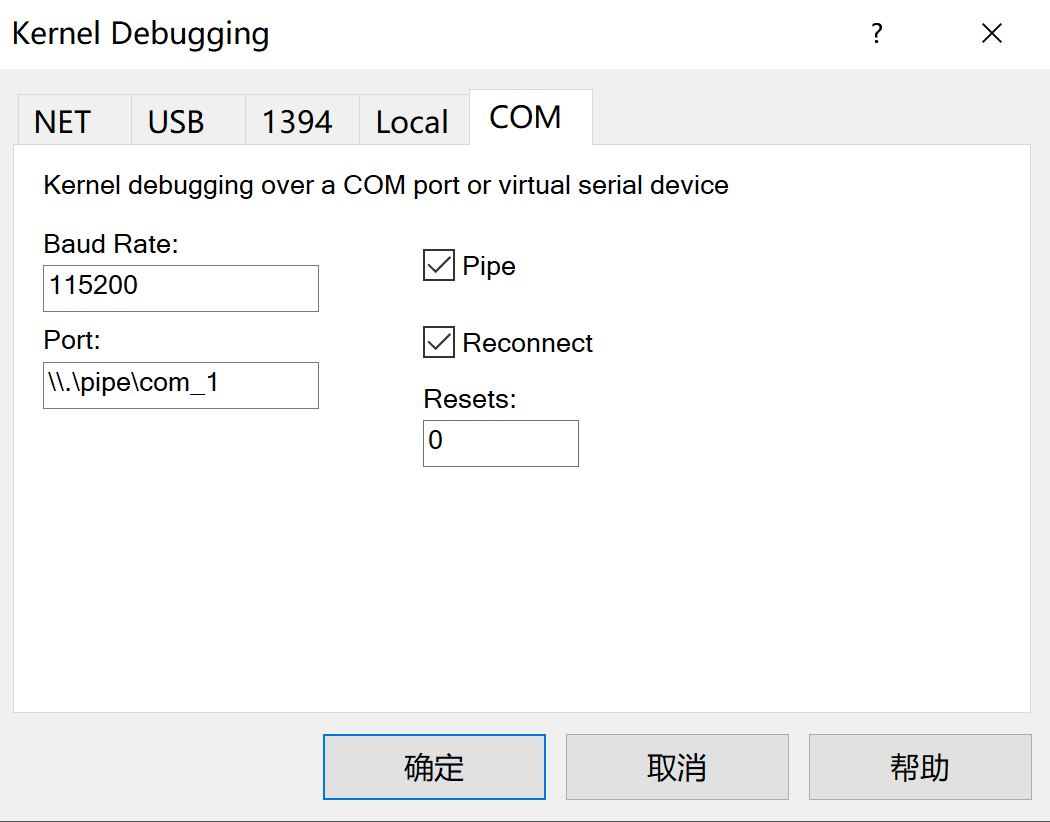
照样配置好
然后能看到回显
下面点击break
这边已经连接上了
然后设置断点
1 | |
bp DancingKeys+0x8000
接下去输入g
让虚拟机运行
然后加载驱动
本来是想c语言写了编译运行后加载驱动
但是失败了
后来问了下夜影师傅。。。。。。成功填坑
下面就是基本调试了
1 | |
驱动学习
学习一波驱动编程
以后可以出点沙雕赛题
当然肯定不会一次性学完的。。。慢慢来
下面是最基本的驱动
1 | |
特别简单啊和linux内核模块编程差不多
一个入口函数和卸载函数
卸载函数不写的话只能关机卸载了。。。
Android逆向
稍微结合着视频教程学了会
大致了解了安卓的架构(不然有时候问问题听都听不懂)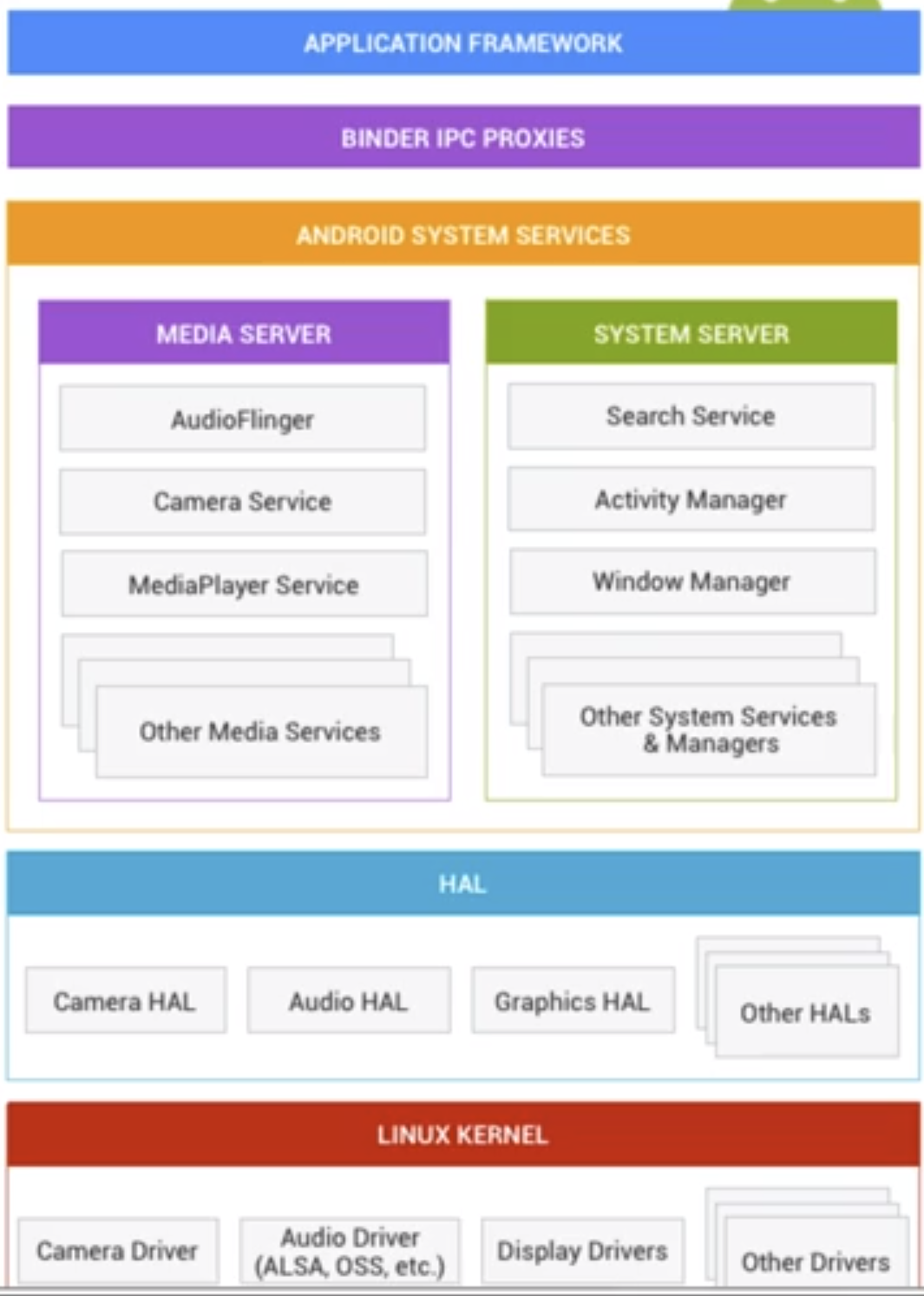
主要还是基于linux内核
还有平时逆向分析中分析native和java层
这个其实早就知道了。。。就是不知道为啥。。。算是填坑了
cnss
cnss是电子科大给新生的一个平台
有道不错的题目可以康康
这道题目过了俩天还是没人出
当时拿到题目算了下时间,30分钟出的flag
难度确实有点,但都是基础可以秒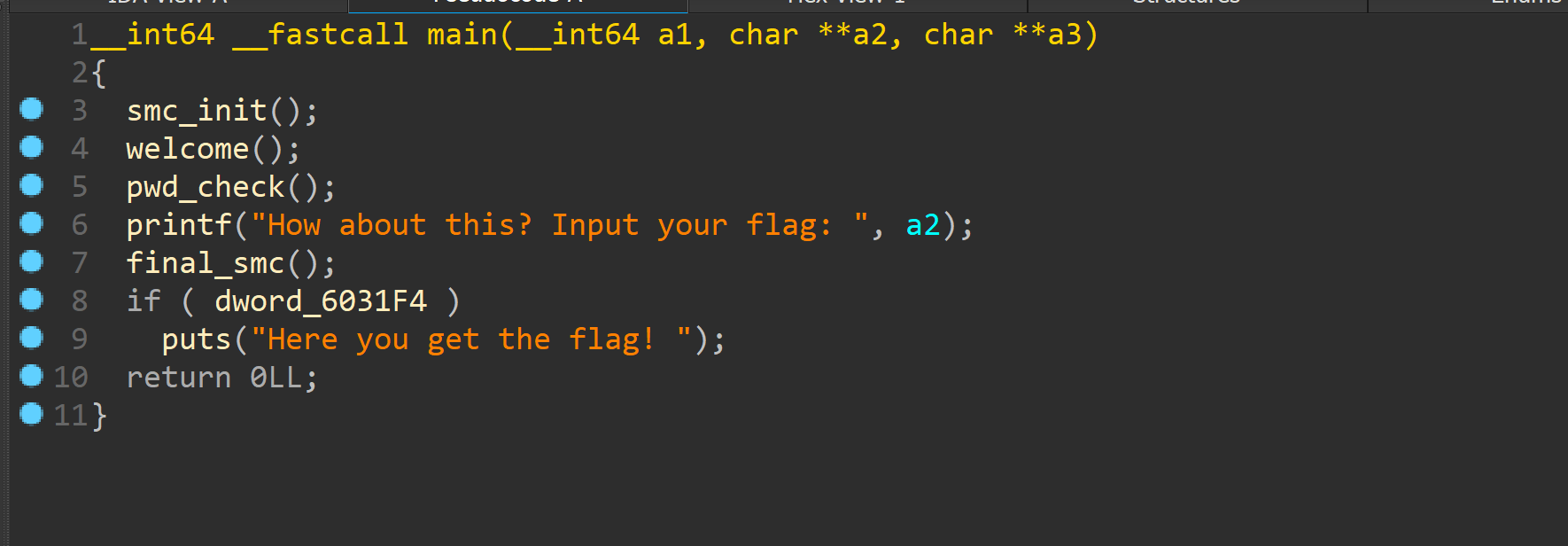
大致流程如上
smc_init中有mprotect函数明显修改权限
下面有个pwdcheck
看下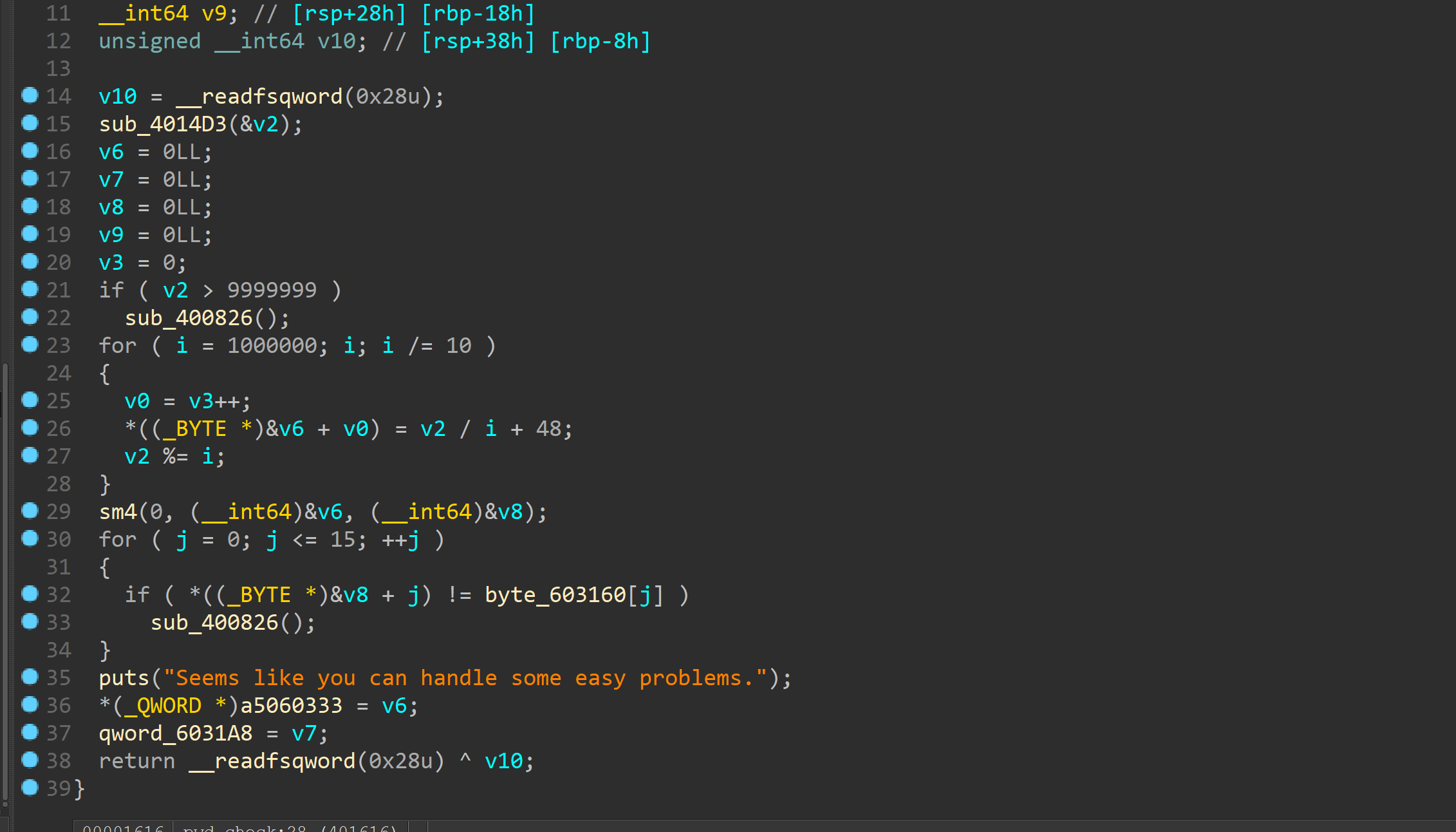
其实是个原装的sm4算法
百度c源码直接解出pwd
key和最终比较都给了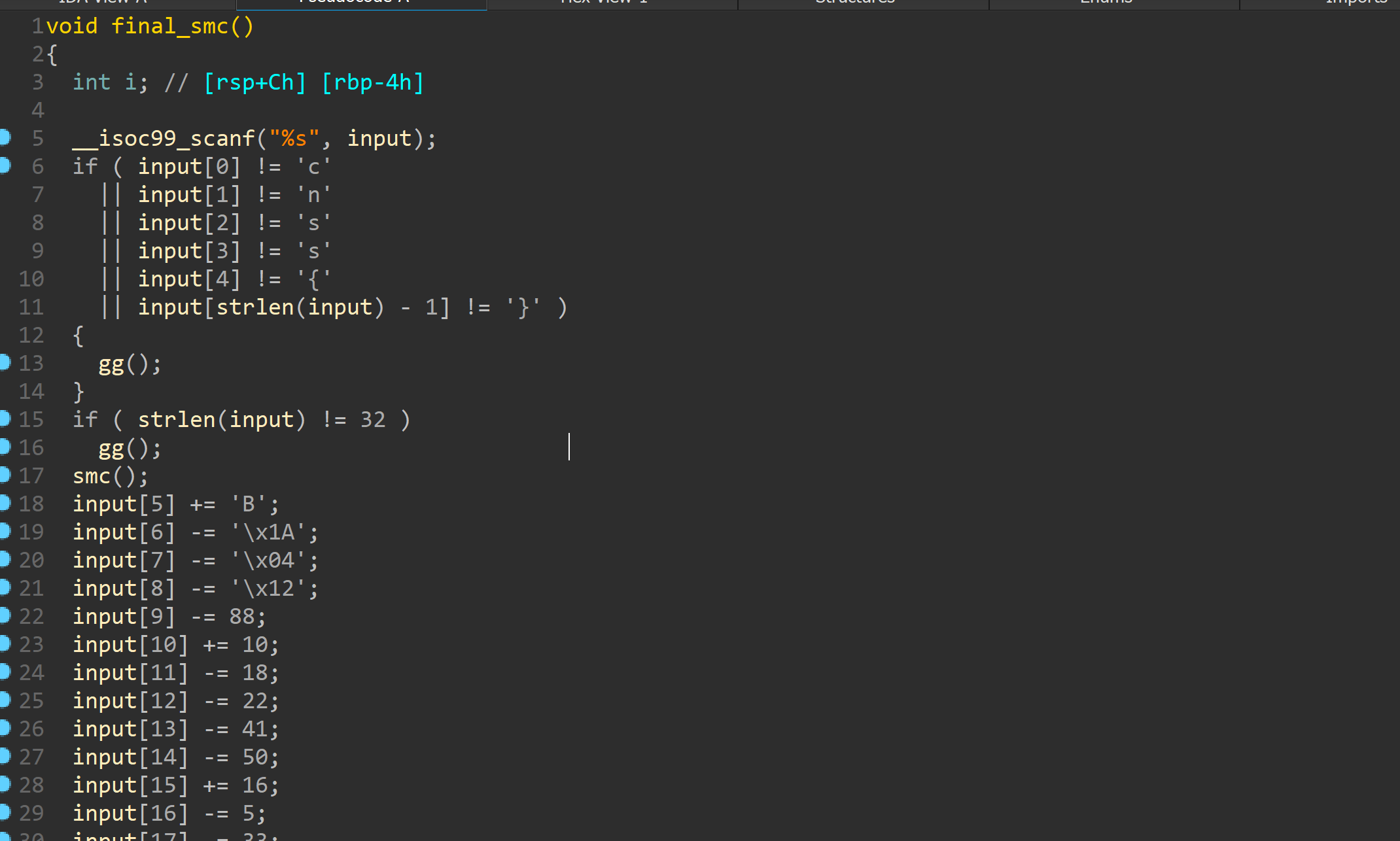
然后是最后的smc操作
看上去操作很简单事实上是迷惑行为
调试发现是个vm
//个人总结了vm的速写法,很快就能看出来在干啥
就是把输入与之前的pwd xor
然后比较
不难,但是能让人眼前一亮
和国赛那个bbvvmm有神似之处
需要对加密算法熟知,当然你即使不知道这是sm4可以直接百度特征码
又上了道题
关于花的
有一说一,这平台题目确实不错,题出的挺好
特别是最近这俩题
说下这个junkcode
1 | |
直接打表解决,我打的表漏了个@。。。但是能猜出来
主要的花是俩种
一个是call影响栈指针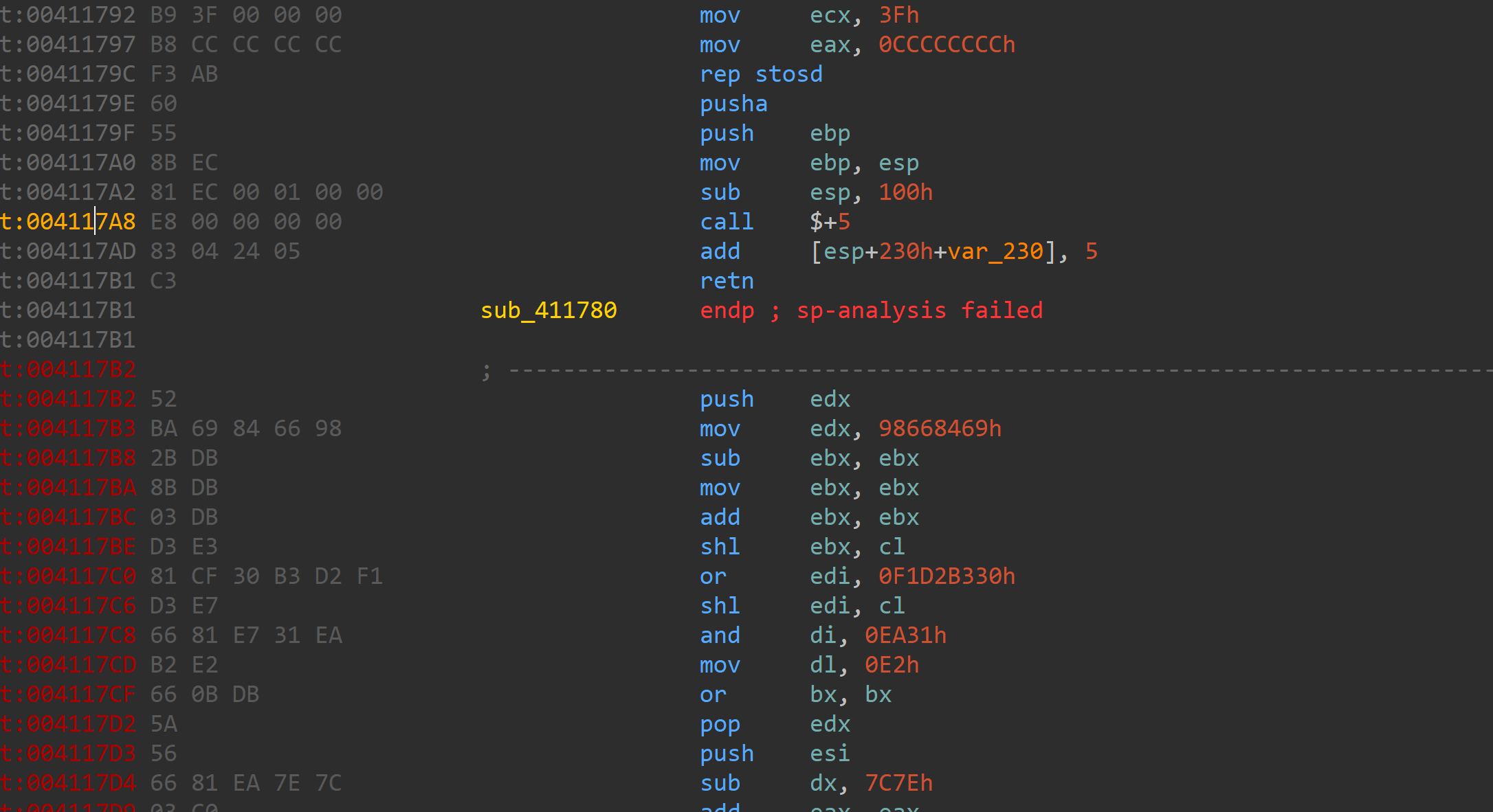
还有一个就是普通的垃圾填充了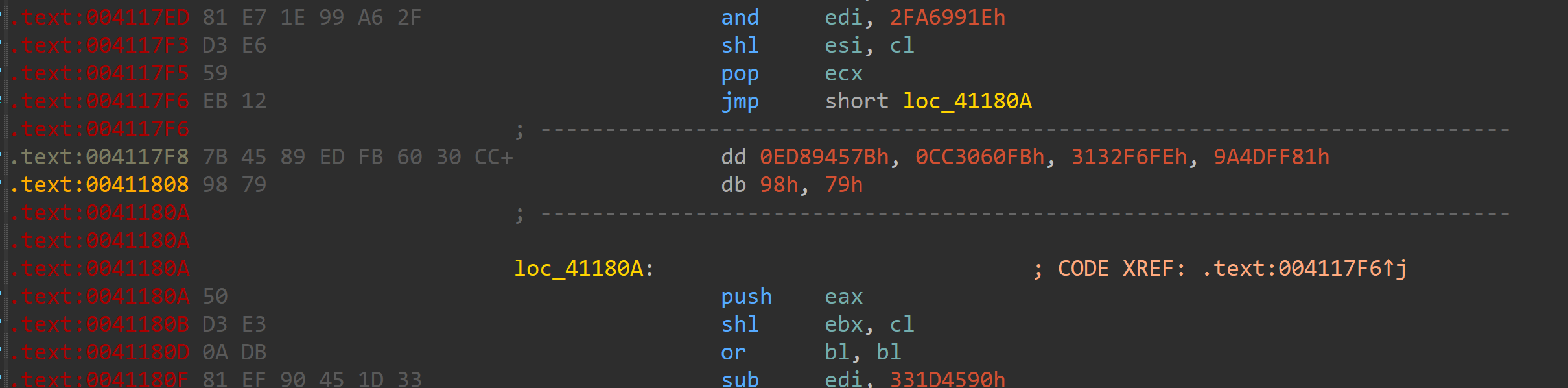
全部填充nop即可
1 | |
jmp的辣鸡代码写不出脚本。。。如果单纯匹配机器码的话有其他指令也会存在0xE8
然后就是具体判断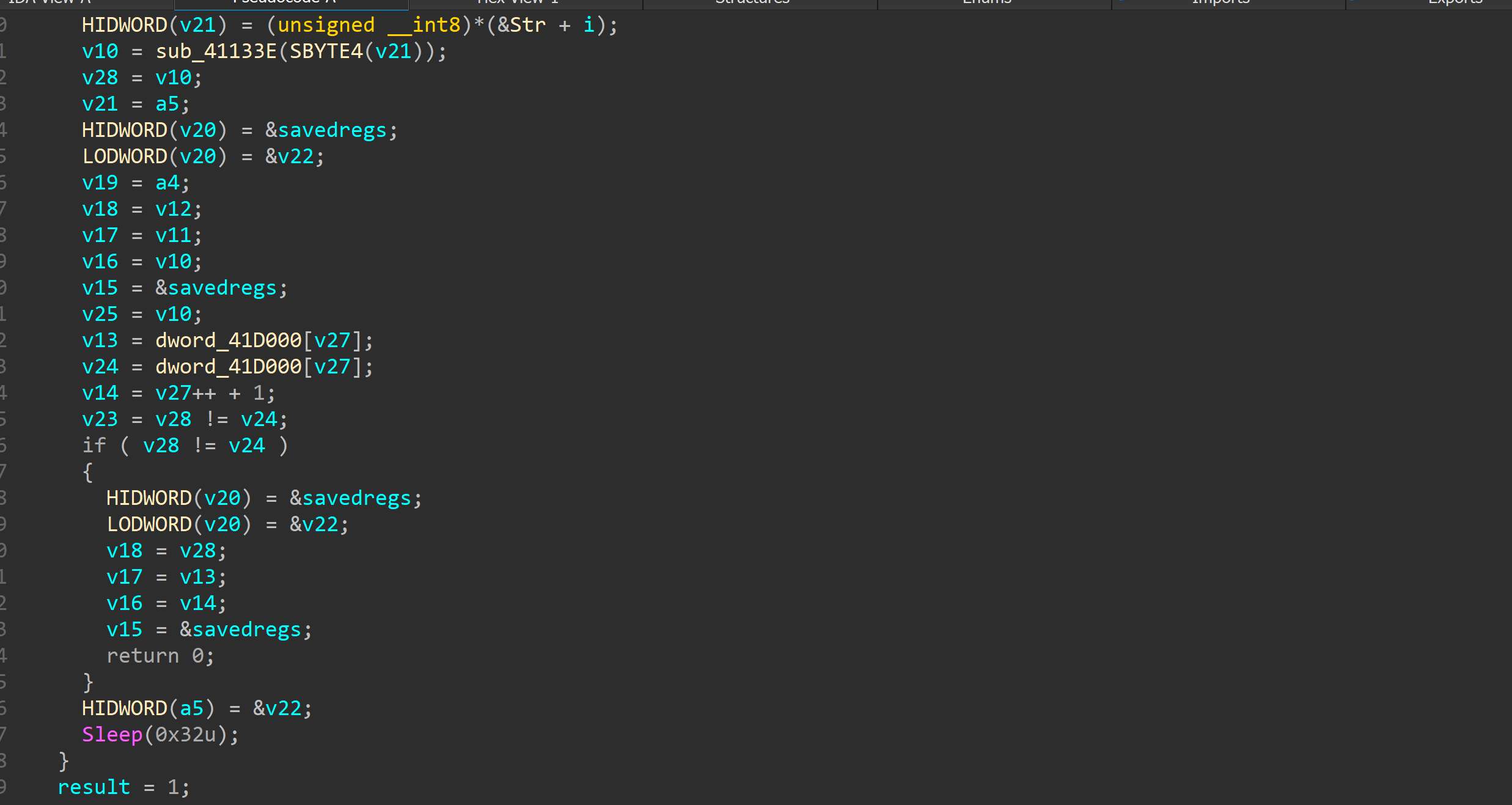
就在这
具体加密在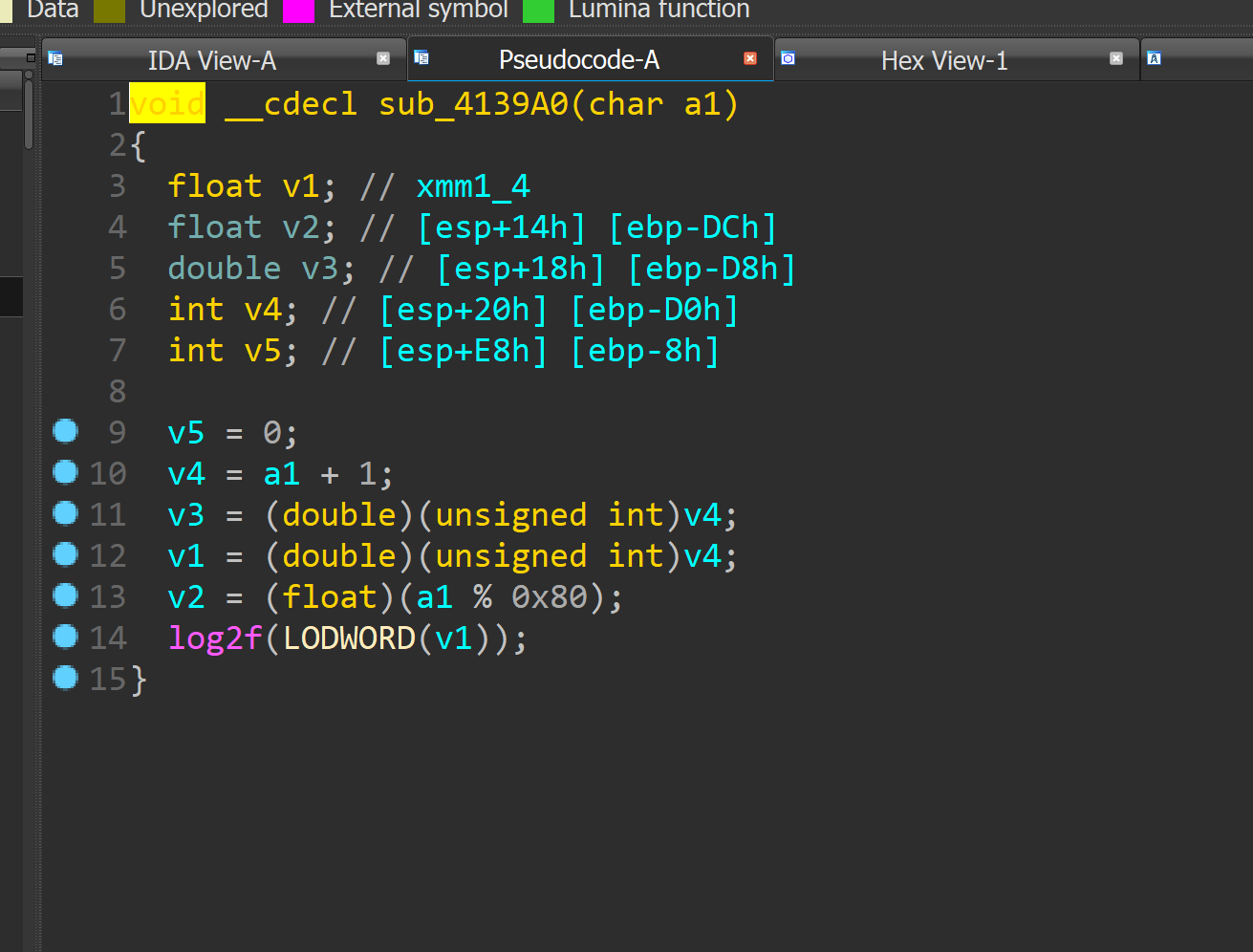
观察汇编即可发现每次加密一个字节
加密完就比较
所以可以打表来写这题。。。
但这也正是这题想表达的junkcode,题目出的挺不错的。
如果加密出的难一点可能会死一片
好在是exe,换成elf angr一跑就出
又上了一题
我佛了
暂时日不出。。。
主要是壳。。。
upx 3.95最新的壳
估计改了什么东西。。。
//以前遇到壳直接脱壳机的我现在gg了
但是upx -d还是能脱但是不能运行
不像是自校验。。。
静态分析发现有花,花还是好去的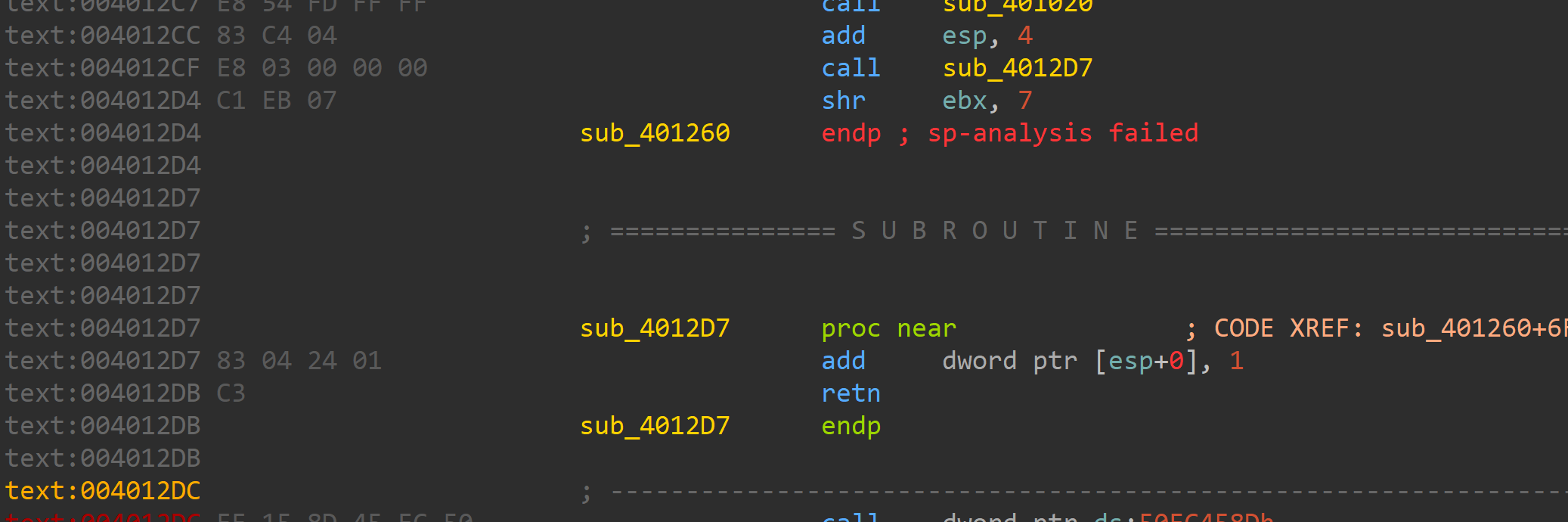
就是返回到shr ebx, 7指令+1处
直接patch完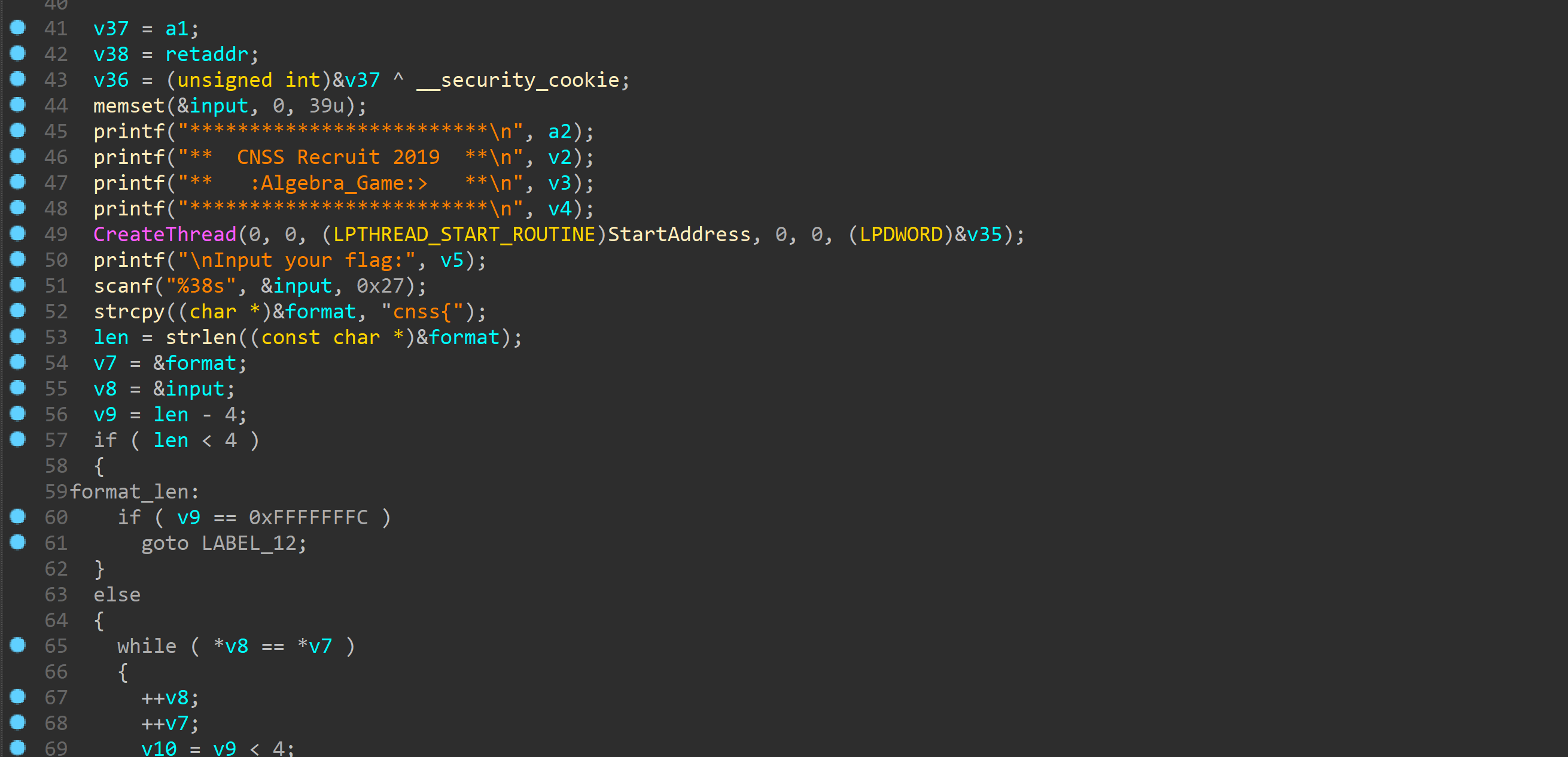
可以看到大致流程是先判断是不是cnss{}格式
长度为38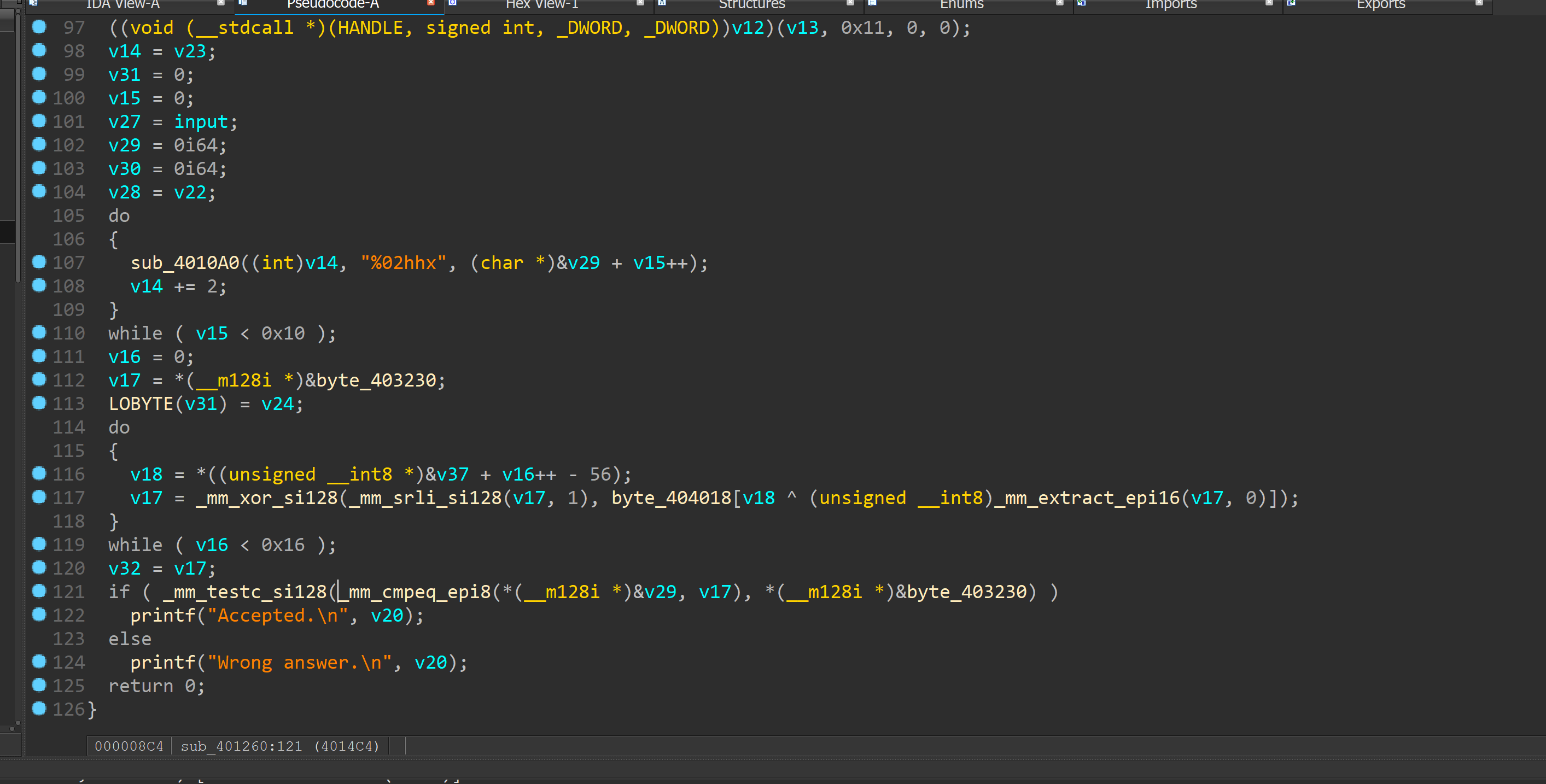
然后进行取表后xor操作。。。
最后直接比较判断。。。
由于不能调试很蛋疼。。。看不太懂。。。
没办法,只好去学一波脱壳了
//day2
脱壳是不可能的
这辈子都不可能的
调试了一波
发现有类似反调试的东西,直接忽略了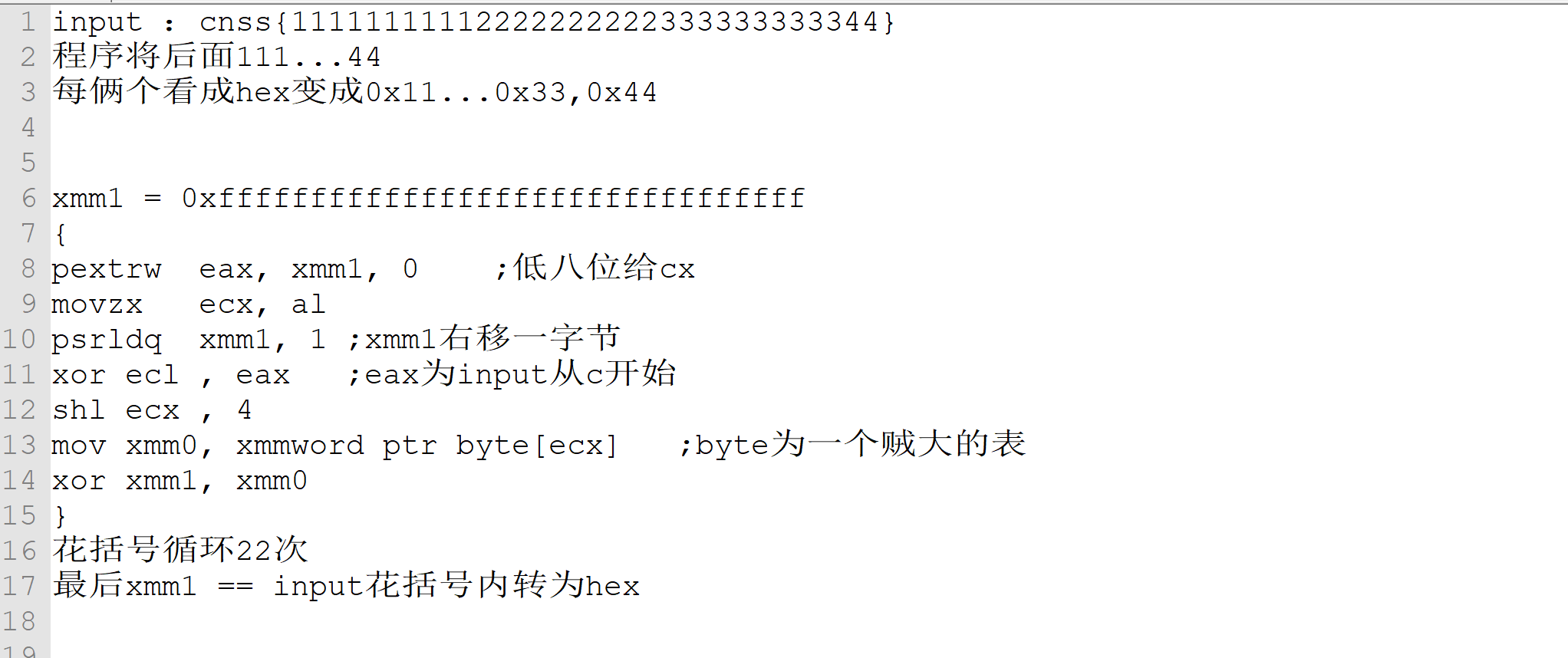
看完后整体逻辑大致如上
有一种crc128的感觉
实在不知道怎么逆向
问了下出题人果然。。。就是个crc
学一波crc
//10.20
打巅峰极客比赛暂时咕咕咕
看了波crc32感觉逆不了
后来得知当消息长度小于等于验证长度即可逆向。。。
佛了,赶紧学一波
好吧。。。tctf 2019原题
是个密码逆向。。。搞不来
roarCTF
逆向签到。。。实在太菜了后面写不出啥
polyre
是个很恐怖的ollvm。。。
学到了点新东西
拿到ollvm的题一般我都是猜。。。
扫了一眼大致看了看判断在memcmp那
下断点输入一堆a发现每8个byte出现了重复
那就是说每8byte加密一次
然后具体看看啥加密
在所有有操作命令处下断点然后看。。。发现是把每八个输入看成long int
然后不断地*2 ^0xB0004B7679FA26B3LL
调试了发现没有规律可循就懵逼了。。。当时才打完公测。。。比较晕
就没有继续看,后来在学长的告知下发现有个工具。。。
以前看过那个腾讯安全发的文章。。。然后工具不能用
后才来知道怎么用。。。
用工具反混淆后好看了很多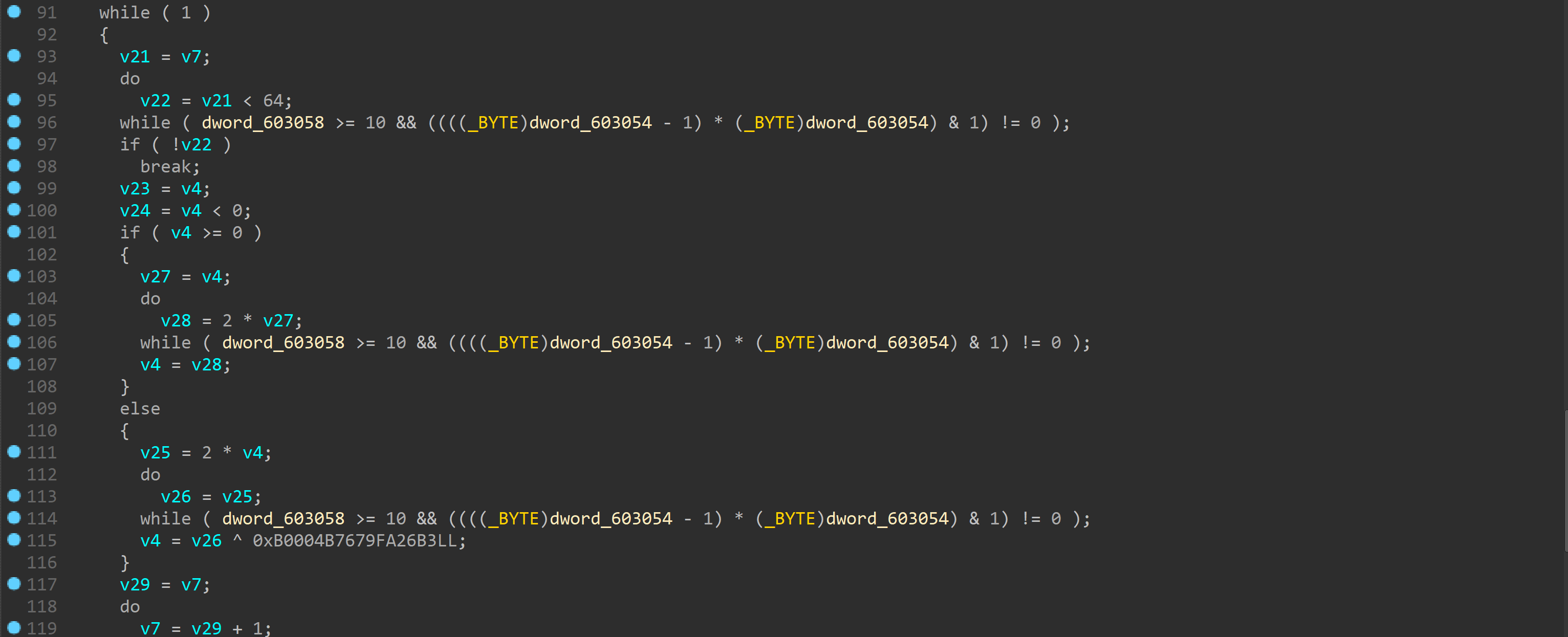
其实是看成了signed long int
然后判断是否大于等于0
大于则乘2
否则乘2后xor
64次后进行比较
因为有溢出。。。写逆算法时懵逼了
后来发现可逆。。。通过判断奇偶来选择高位补
裂开来
Tank
开坦克。。。
直接看dll
主要逻辑就是爆破,当时逻辑分析出来了就是不知道为什么写脚本一直有问题就没有爆破出
后来还是整出来了
我佛了
1 | |
python写代码能力还是不怎么厉害啊
当时好像是因为加密的时候是个list才导致爆破不出
应该改成str的
中科大校赛
难
KVM
又看到了kvm
看来这个坑必须填了
我佛了
参考链接
https://www.cnblogs.com/Bozh/p/5753379.html
1 | |
创建kvm句柄->创建vm->分配内存->加载镜像到内存->启动线程执行KVM_RUN.
所以一般都是看拷贝的机器码来分析
hlt代表退出
这题可以看出是个tea
//我傻了没有运行。。。发现就是写好解密函数
调用号自己改就行
1 | |
直接爆破
flag{KVM_i3_4_b4sic_linux_c0mp0n3nt_k3rn3l_supp0rt_vm}
过几天再写写xnuca的
当时没写出来
巅峰极客
有一说一,感觉这比赛质量不太行
俩到re
一道二血
还有一道和roar的tank一模一样的套路
我都佛了
说一下第一道吧
flodbg
就是个花指令加反调试题
完全不存在加密算法。。。说实话也太简单了吧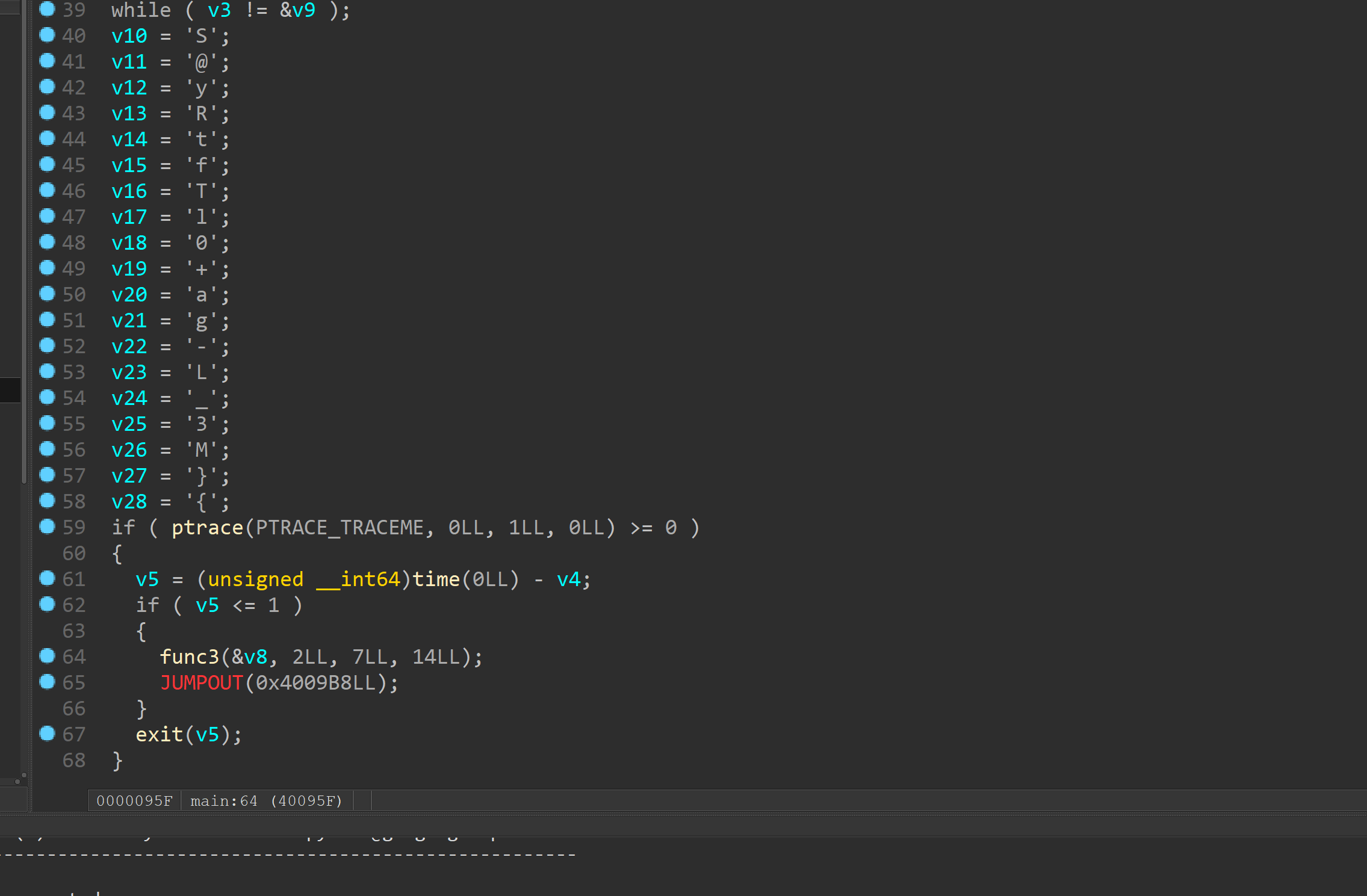
time什么的反调试直接patch即可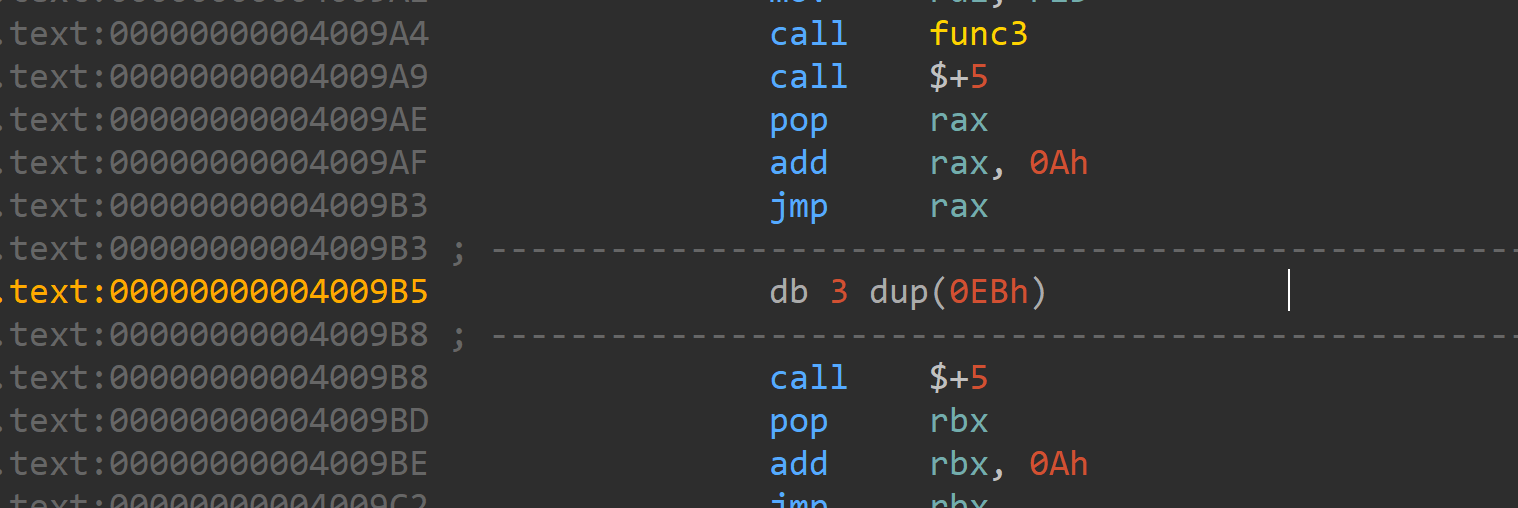
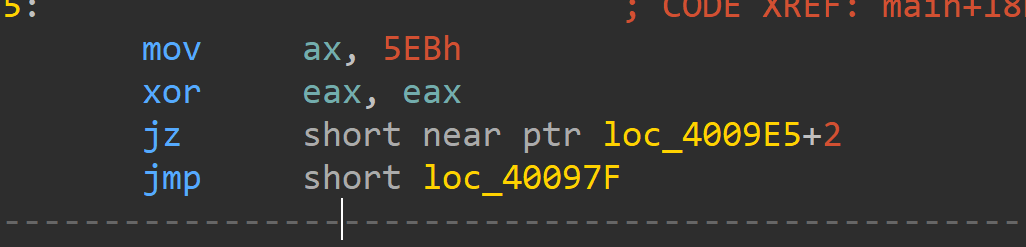
花指令主要是像上面的俩种
很好去
然后调试就能猜出func3是个类似栅栏的函数
他不改变你输入的值只是单纯移了下位
那就简单了输入0123456789abcdefgh然后把对应位还原即可
1 | |
NCTF 2019出题记录
难看的代码
源码奉上
1 | |
出题思路:
主要考察新生对ctf中常见的对抗逆向技术
分别是
anti_debug
Smc
Junk_code
加密部分写的不怎么复杂就一个TEA加上一些加加减减。
这些对大型比赛来说也就是个签到题把//或者签到题都算不上
源码解析:
前言:这是我六个月前第一次出题的代码有很多不足,有些还待改进。
有部分需要修改
exit_0是antibug中会使用到的
主要是对change函数开头赋值成exit(0),故机器码需要根据最后生成的可执行文件修改。
还有就是花指令部分,生成完我才发现jmp的那个花指令没有起到我想要的效果,直接修改机器码E8(call)。
另外就是smc部分我只写了解密,生成完后肯定是不能运行的还需要patch,写脚本来加密,实现起来也不难。Idc即可
1 | |
关于check部分一开始check了格式//事实上是多次一举,后面tea后又check了全部flag
还有就是strlen函数我发现有一个很不好的地方
套用在for循环中时,每一次都会check一次strlen,这样就出现一个问题,就是当tea后密文出现0,这样strlen就会被有差错,当初我设定的flag时nctf…然后加密一轮后出现0,直接不加密了,时间问题没有好好优化就把开头改成了NCTF,其实改成24就行,毕竟前面已经限制了长度必须为24
还有就是花指令部分
主要出现了俩种花指令,一种是栈指针还有一种是jmp的。
反调试部分我才用使用汇编来写,这样的话ida不会反编译出函数,比如antidebug2其实就是isdebuggerpresent而Ida并不会识别出该函数。
smc部分我采用了double_smc,这样就不能通过data xref来追踪。但是意义不大。。。熟练的人一下就能看出,smc部分出现的anti_debug,下面printf一句debug everyday可以一下看出这是反调试函数,但是如果不仔细逆向直接把该函数patch的话到change函数就直接exit了,里面紧跟着的又是一个反调试并把之前保存在exit的值重新赋给change开头
AES
面向字节的密码
state:4*4矩阵(key 128位,列数为6/8当key为192或256时)
addroundkey
状态矩阵与子密钥xor
密钥编排
state每列四个进行操作
第四列(key4) key5 =(key4)rotword —> subbytes —> xor key1
key5 —> xor key2
。。。
每四次一次rotworld subbytes
subbytes
s_box s_box-1 互逆
对应取值为在GF(2m)中的逆元经过仿射后的值
比如c2逆元为2f经过仿射后为25就是S(C2)的值
S(A)=B
非线性:S(A+B) != S(A)+S(B)
扩散层
将单个位的影响扩散到整个状态,且都为线性操作
也是fault的写法
shiftrows
将状态的每行左移
第一行不变
第二行移1
第三行2
第四行3
不改变值
mixcolumn
和固定矩阵相乘,扩大字节影响范围。
具体乘法实现是在GF(2^8)中实现的
逆向mixcolumn
乘上在伽罗瓦域上的互逆矩阵
逆向shiftrow
可以理解为rightrow
逆向subbytes
sbox逆操作先仿射变换逆然后求解逆元即可
AES_DFA
例子:round9
在最后一轮mixcol之前出现了单字节fault
经过mix和shift等操作影响到四个字节
和正确密文xor得出表达式可进行约束求解
对于aes128需要每列俩个fault数据,足够可约束出key10的4个byte
所以总共需要8组fault数据和一组正确密文
这样就能够求出key10
然后就能反推密钥编排求出key
XCTF-FINAL 2019 FAULT
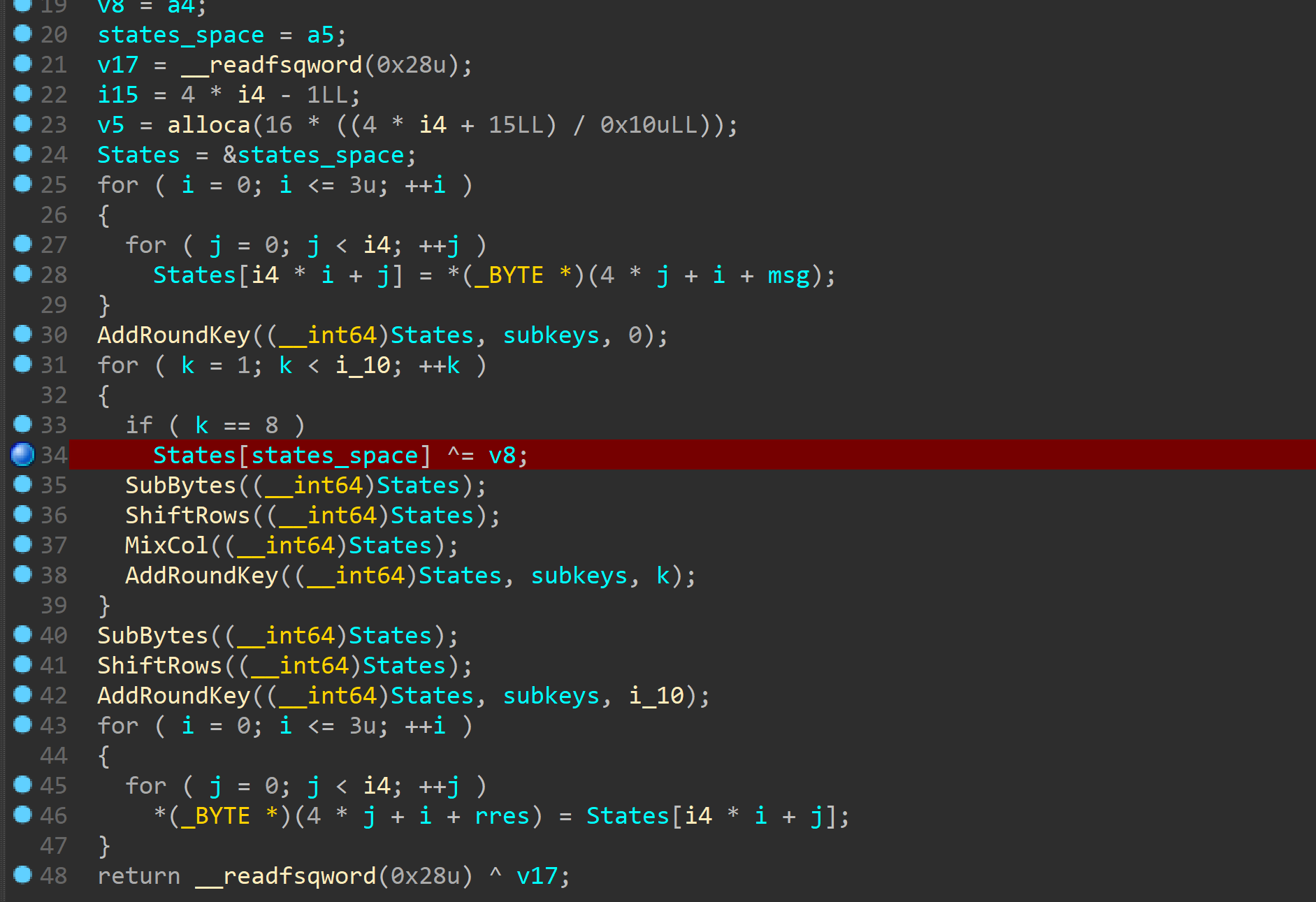
可以看到aes这部分出现了一个很明显的问题
再最后俩次mc之前有一次xor
这样就会产生fault
经过俩次俩次mcfault影响到16字节
v8是0,但是可以通过利用溢出来修改
获取俩组错误密文和一组正确明文就可以求解出key10
然后key就可以求出来了
看了下其他队伍的wp发现貌似还有其他的写法。。。
直接利用printf打出来那种。。。
哎。。。太菜了
学了波数学算是搞懂原理了
RSA加密与解密
平方乘法
快速计算指数的方法
指数用二进制表示
初始化平方
如果为1
平方后mul
如果为0
直接平方
原理其实就是在逐位复现二进制
中国剩余定理
没怎么看懂。。。
但是百度了下发现是求解同余方程的
寻找大素数
费马素性检测
用费马定理推,不满足则为合数
满足则可能为素数
//特例是卡迈尔克数
Miller-Rabin素性测试
p = 2^x * r
a^r = p-1
a(rand) // count = s
Diffie-Hellman密钥交换
选择大素数p与整数a
p作为模数
甲方选择key1
乙方选择key2
a^key1 mod p -> 乙方
b^key2 mod p -> 甲方
然后再一次的指数运算
这样双方的值就相同,即是传输的key
代数知识
群
群指一个元素集合G以及联合G内两个元素的操作o的集合。
1.群操作o是封闭的,对于ab in G ,aob in G始终成立
2.群操作可结合
3.存在一个元素1 in G,对所有的a in G均满足ao1=1oa=a,这个元素称为中性元或单位元
4.对每个元素a in G,存在一个元素a-1 in G,满足aoa-1=a-1oa=1,则a-1称为a的逆元
5.对所有的a,b in G 都额外满足aob=boa,则群G称为阿贝尔群或可交换群。
元素的阶
a^k = 1 mod n
k为阶
循环群
有限群
一个群是有限的仅当他拥有有限个元素群G的阶或基可以表示为|G|
Zn,+的基为n
Zn,·的基为n的欧拉函数,Zn是由小于n且与n互素的正整数的集合
元素的阶
a^k=1 k为阶
循环群
群G包含一个有拥有最大阶的a=|G|,就是循环群,a为原根(本原元)或生成元
对于每个素数p Zp都是一个阿贝尔有限循环群
有限循环群G的本原元的个数为|G|的欧拉函数
|G|为素数时,a!=1的元素都是本原元
子群
(G,o)是个循环群,则G内每一个满足ord(a)=s的元素a都是拥有s个元素的循环子群的本原元
拉格朗日定理
假设H为G的一个子群,则|H|可以整除|G|。
//todo
基本协议
Bob公开keypub 对消息x进行哈希函数生成z,然后用keypri对z进行签名为s,收方Alice验证s解密后是否为z即可。
哈希函数的安全要求
1.抗第一原像性(单向性)
2.抗第二原像性(弱抗冲突性)
3.抗冲突性(强抗冲突性)
弱抗冲突性
鸽笼原理证明了弱抗冲突性对于哈希函数来说必存在。所以需要满足的条件就是正向容易逆向难,给定x1与其对应的哈希不能找到消息x2生成同样的哈希
强抗冲突性与生日攻击
生日攻击简介:
至少出现多少人才会出现生日冲突概率大于1/2
答案是23个
不冲突概率为(1-1/365)(1-2/365)。。。
用1-该值即可
当40人时,冲突概率达到90%
生日攻击是对所有哈希函数的通用攻击,该攻击的存在决定了哈希函数的输出位数至少为128位
测试数据至少约为2^(n/2)
n为位数
对于主流哈希函数还有更快的攻击就是数学冲突攻击
哈希函数概述
专用哈希函数MD4家族
主要指转为哈希函数而专门设计的算法
对称密码学与非对称密码学
对称密码学
存在问题
1.密钥的分配
因为信道不安全
2.密钥的个数
对于一个很大的网络需要存储的密钥有很多对
3.不可实现不可否认性
非对称密码学
key分为公钥与私钥
公钥公开,用户用公钥加密数据后,收方可用私钥来解密
具体的实现需要一个单向函数
准确来说就是逆运算即使用已知的最好的算法也需要花费很长的时间,但是正向运算足够快。
目前来说满足的只有大整数分解问题,离散对数问题还有椭圆曲线。
数学知识
欧几里得算法
gcd(最大公约数)
求解最大公约数通过mod迭代直到为0即可求得最大公约数
扩展欧几里得算法
在欧几里得算法的基础上将最大公约数以线性的方式表示
求解逆元
逆元存在条件当且仅当gcd=1即互素
求解a mod b的逆元可用EEA表示gcd
然后对应a的系数就是逆元
欧拉函数
相应环内与之互素的个数
如果m可因式分解那么就有公式可以套用
费马小定理与欧拉定理
费马小定理
a为整数p为素数
则a^p = a(mod p)//a的p次方
推广到整数就是欧拉定理//使用条件是a与m互素
a^o(m)=1modm
费马小定理就是欧拉的特殊情况//当p为素数时
基于分组密码的哈希函数
输入分组进入压缩函数迭代
输出为最后一轮压缩函数的输出
// Merkle-Damgard结构
红帽杯
re1
题目名称是xx
可以想到是xxtea
首先程序检查输入长度是否为19然后进行一次xxtea加密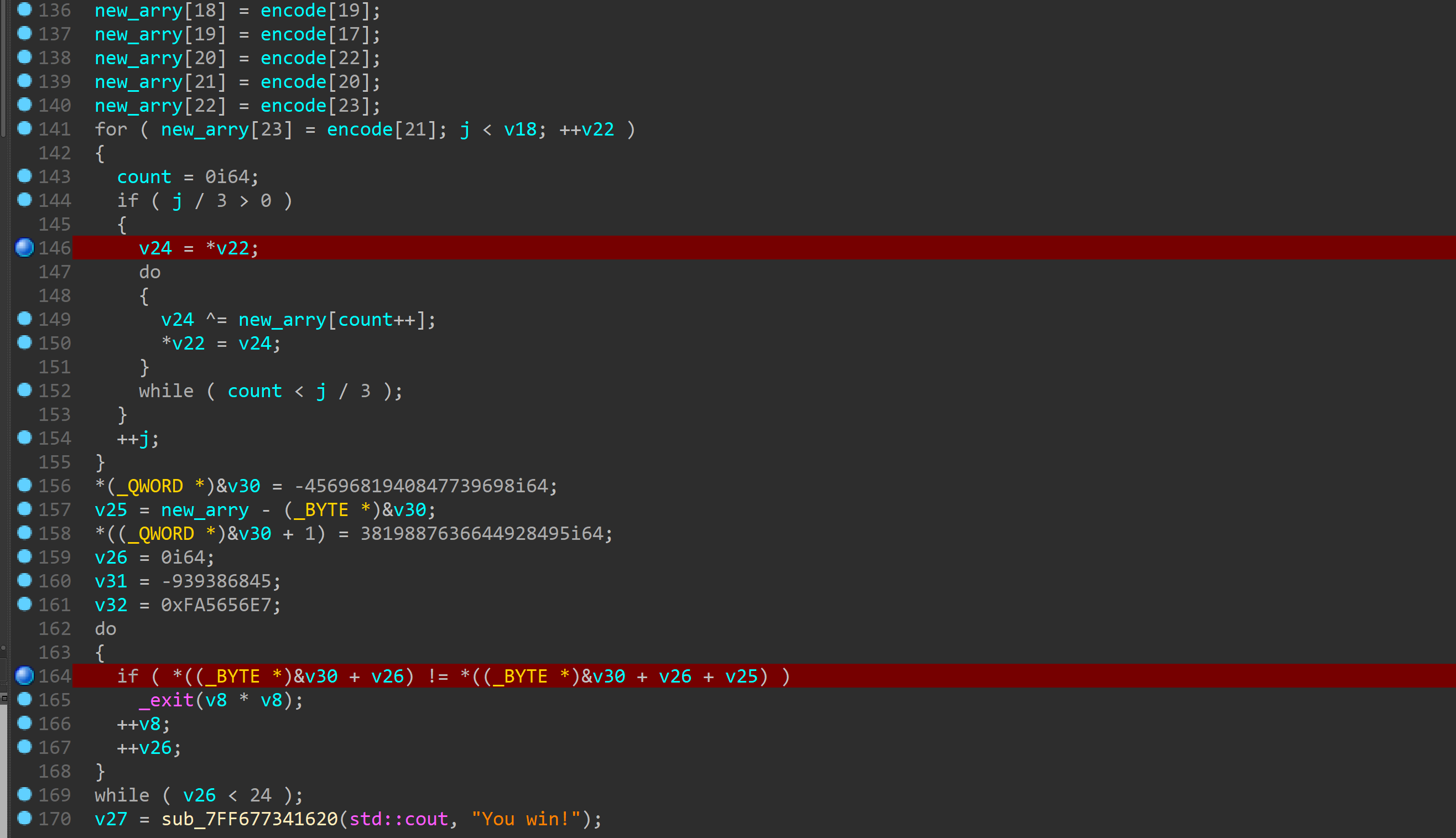
加密的key是输入的前四个字符
然后有一个换位xor的操作逆过来整一下就行了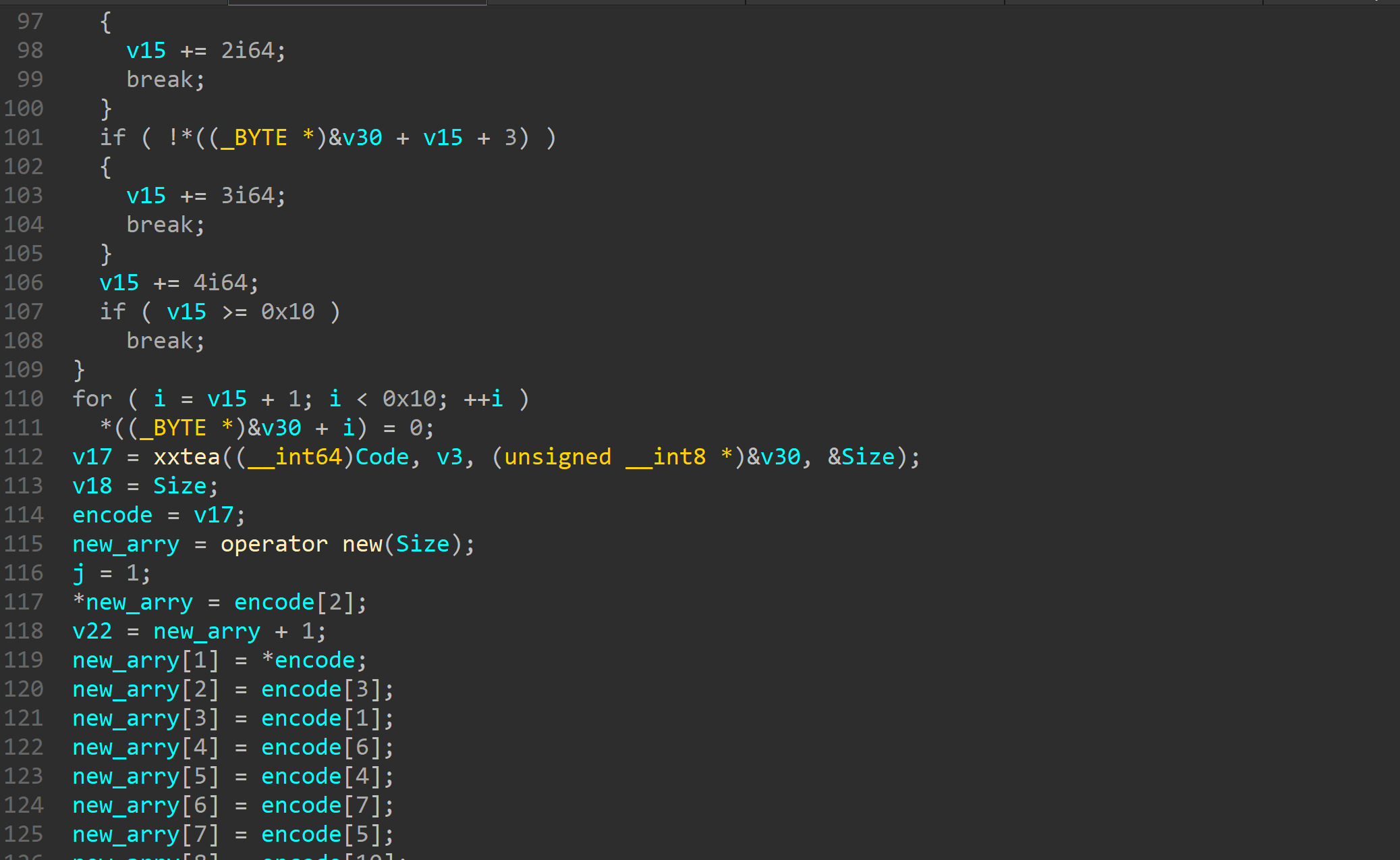
1 | |
re2
没怎么逆
看的时候听学长说貌似要看sub_400D35函数
当时没多想点进去看了下就是个xor
和key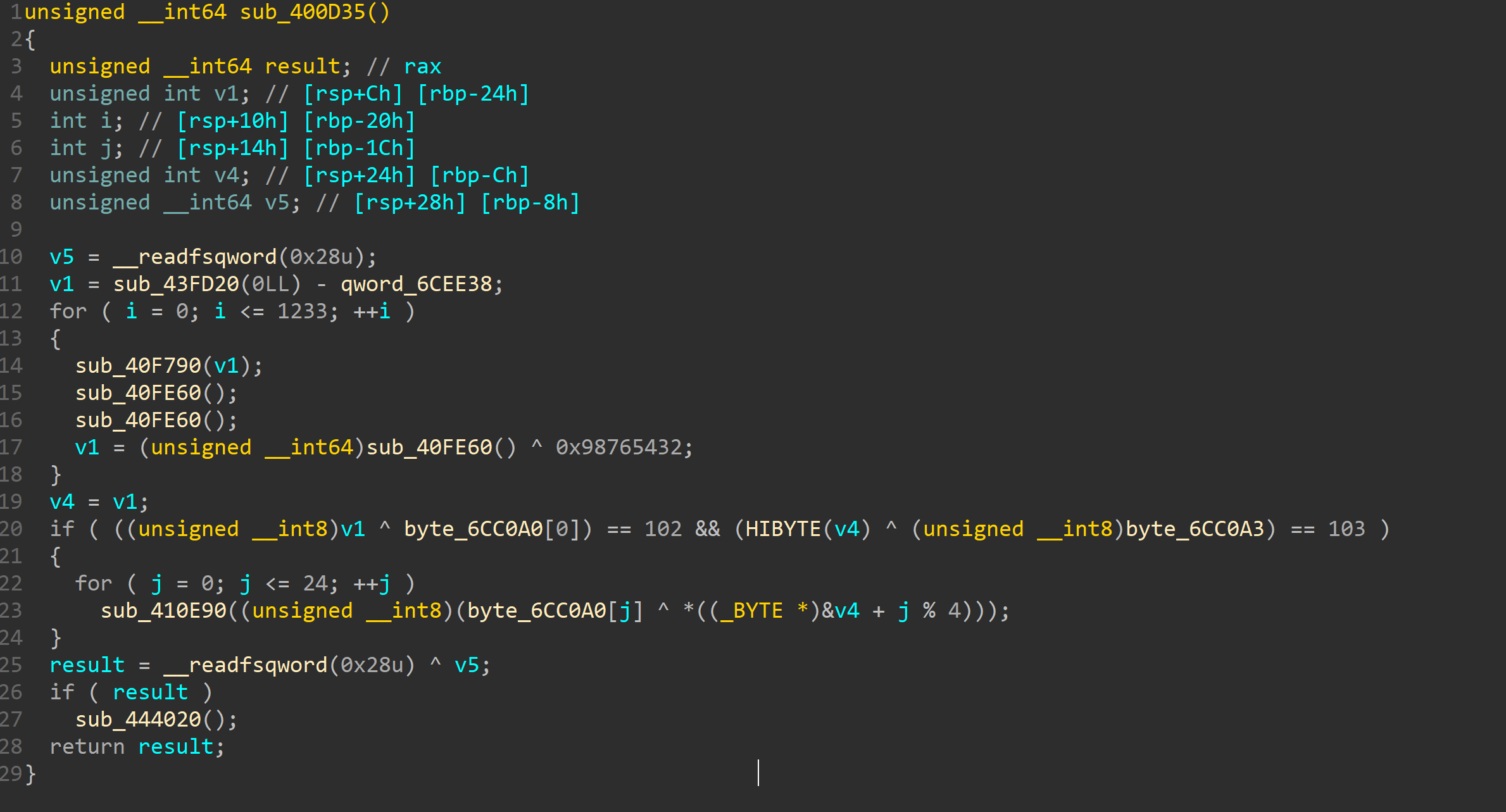
看了下发现还是猜
第一个xor后为f
第四个为g
那不很明显flag吗
猜一下然后xor就行了
1 | |
后来仔细看了下一开始对你输入进行了xor i比较
解一下
1 | |
然后又一次输入
对第二次输入进行一堆base64解密
直接比较
发现为
https://bbs.pediy.com/thread-254172.htm
然后就没了????????????
在sub_400D35下断点发现断下来了
看来还是会跑过去
但是与输入无关。。。和时间相关
1 | |
最后发现是这个考点。。。
打pwn的肯定知道
re3
三次输入
中间有sleep直接给patch了
先对输入进行了平方 FF0是pow函数
然后是乘4 A90是mul函数
然后对第二个输入
乘3
平方
对第三个输入
他先用7 * input3
然后result**input3
我佛了
下面是对输入的判断
input2<input1<input3 //应该是这个,没有仔细看
然后对三个输入之间进行一些蛇皮操作后就来最终check了
对了就有flag
//check大小完后的操作
550函数为add
7E0函数为del
1 | |
最终化简是x*3+y3 = z**3+42
https://www.sciencealert.com/the-sum-of-three-cubes-problem-has-been-solved-for-42
google即可发现答案
re4
主要函数是
UnDecorateSymbolName(v5, outputString, 0x100u, 0);
反修饰
下面的验证直接爆破
1 | |
private: char * __thiscall R0Pxx::My_Aut0_PWN(unsigned char *)
发现反修饰后应该如上
下面就是修饰了。。。
只能百度一波来自学
发现为?My_Aut0_PWN@R0Pxx@@AAEPADPAE@Z
置换一下
1 | |
输入为
Z0@tRAEyuP@xAAA?M_A0_WNPx@@EPDP
re5
unity逆向
又是游戏,当我看到这个的时候已经猜到了。。。
打开csharp的dll一顿乱翻然后要爆破什么sha1爆破sha256
结果。。。翻了一波dll感觉很正常是在实现程序流程
最后随便翻翻发现Interface.dll里面有点神奇的东西
可惜是c++写的看起来烦死。。。
不知道怎么调试,后来acd说可以用win自带的什么rundll32
可是佛说 不行
后来问了骑驴才知道可以写程序直接加载dll库调试…
后来看了大佬的博客发现更好的代码
上一波大佬的代码
1 | |
运行爆破即可
1 | |
上面的是骑驴的
适合普遍dll
可以进去调试
//貌似在逆核的dll注入那有类似代码
//当时调过,但是没怎么在意。。。现在学到了
虚拟机环境崩溃小记
以后我绝壁保存快照。。。
安装好虚拟机和vmware tools后
首先更新源
具体看下面链接
https://mirrors.tuna.tsinghua.edu.cn/help/ubuntu/
然后开始美化
下载unity-tweak-tool,可能会提示找不到。。。这就需要添加源了
添加源
sudo add-apt-repository ppa:noobslab/themes
sudo add-apt-repository ppa:noobslab/apps
sudo add-apt-repository ppa:docky-core/ppa
sudo apt-get update
sudo apt-get install unity-tweak-tool
然后安装dash-to-dock
https://extensions.gnome.org/
完事。。。各种比例啊美化整一下
差不多就完事了。。。工具什么略
密码学学习
RSA
题目已知
1 | |
用yafu分解n得到下
P1 = 1235542029039790988583258906107
P2 = 1235542029039790988583258906103
P3 = 1235542029039790988583258906163
P4 = 1235542029039790988583258906019
1 | |
easyesa
1 | |
已知
e = 65537
n = 16969752165509132627630266968748854330340701692125427619559836488350298234735571480353078614975580378467355952333755313935516513773552163392952656321490268452556604858966899956242107008410558657924344295651939297328007932245741660910510032969527598266270511004857674534802203387399678231880894252328431133224653544948661283777645985028207609526654816645155558915197745062569124587412378716049814040670665079480055644873470756602993387261939566958806296599782943460141582045150971031211218617091283284118573714029266331227327398724265170352646794068702789645980810005549376399535110820052472419846801809110186557162127
dp = 1781625775291028870269685257521108090329543012728705467782546913951537642623621769246441122189948671374990946405164459867410646825591310622618379116284293794090970292165263334749393009999335413089903796624326168039618287078192646490488534062803960418790874890435529393047389228718835244370645215187358081805
qp = 10450978538445496868237560522155647855468044038637044818500580506745232482415364474390893285539835615564332910332708101539048528242011762736342572650763270501265440674647489375438852377280494520168349154604800218665628586180057648386859933274414030182106920793492451577530884172876623074281199949317487086975
c = 0x71512577b69cea3b42466100f3d5d50de95ab16971ad25d9204ff8df52bd52dafcd054d997ec3fe37d2590c2b0eebec172ec02fa62c35c62e39c89f1f5c51c869a5cc8083c1e76da430f26542a444a0295f52414118e47b72e9f370498cca3a69a1148c9433b97bc816dee45d12fec94f6aaf754273cfb19b0055d5b00630ba1b8a6b2b0a2abfd630d68b7a95e2ec45192e2ff229f893ea6ec7620677d4d8bd79f3dd420e0b2c0a26de37c700a3953c2094c4797bbbb47f72fdc1d8acac69b755d0caeb090885baf7b8e2ea4b36a41bea67477101b9706dedc338e076921c98c8ce2468ab48b14829241dbdfb8572a84714c798a29742b4176061efdf0320c86
1 | |
其实很容易推出公式
RSA3
共模攻击板子
c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291
1 | |
RSA2
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
和上面某题一模一样的写法啊
1 | |
RSA1
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
中国剩余定理
推出公式来解决
1 | |
直接用现成轮子
RSA5
1 | |
模不互素
找到俩组看gcd
1 | |
roarctf rsa
1 | |
题目很短主要还是通过A求得pq
通过开根号即可
1 | |
下面就是约束爆破qp了
1 | |
babyrsa
1 | |
Wilson’s theorem
当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p )
可以观察发现A与B的差很小
通过构造求得pqr
1 | |
pwn
ciscn_2019_c_1
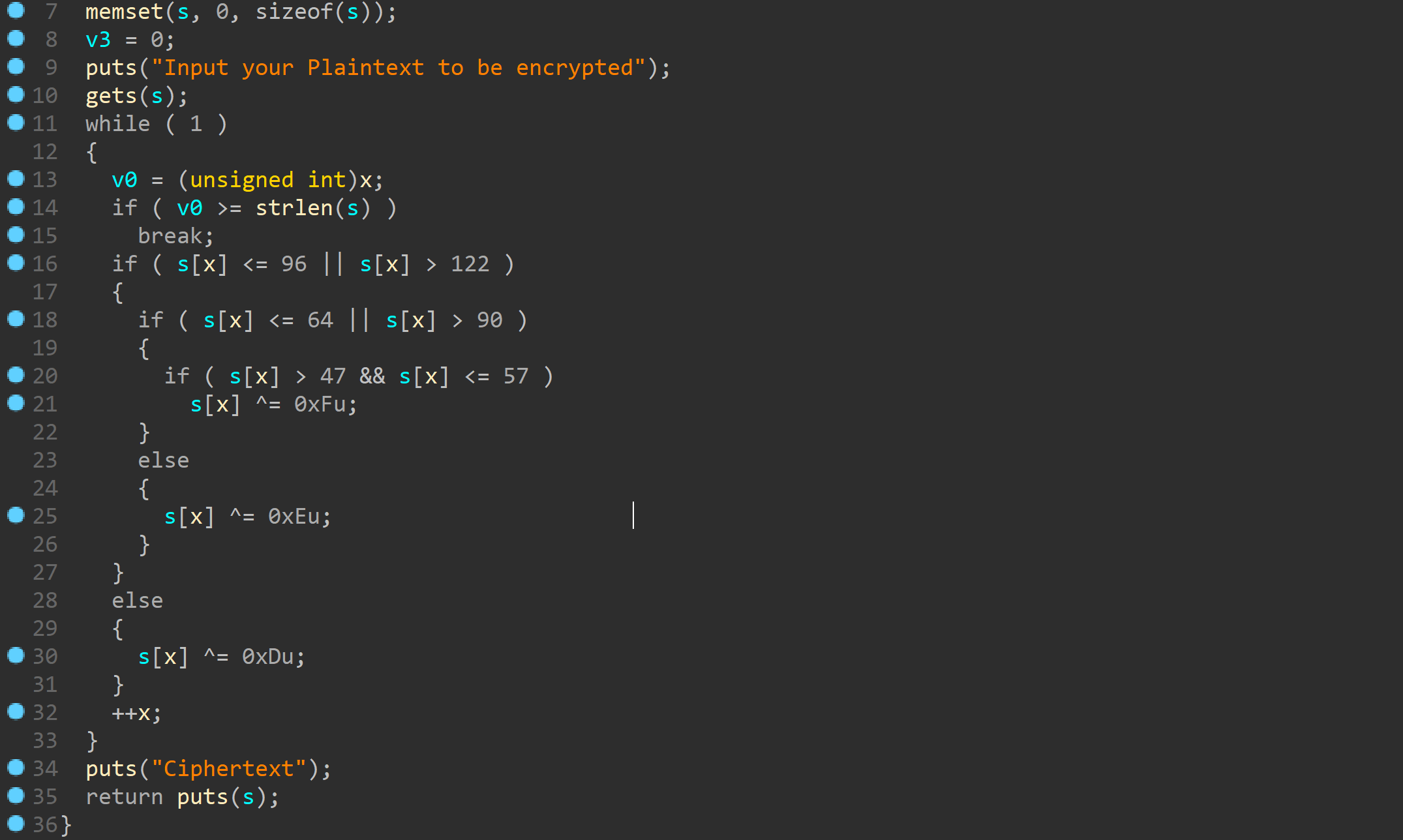
gets函数很明显的栈溢出
这边有个加密部分。。。其实可以构造\0直接绕过strlen
这样就不需要加密了
泄露puts的got表地址后搜索libc即可
1 | |
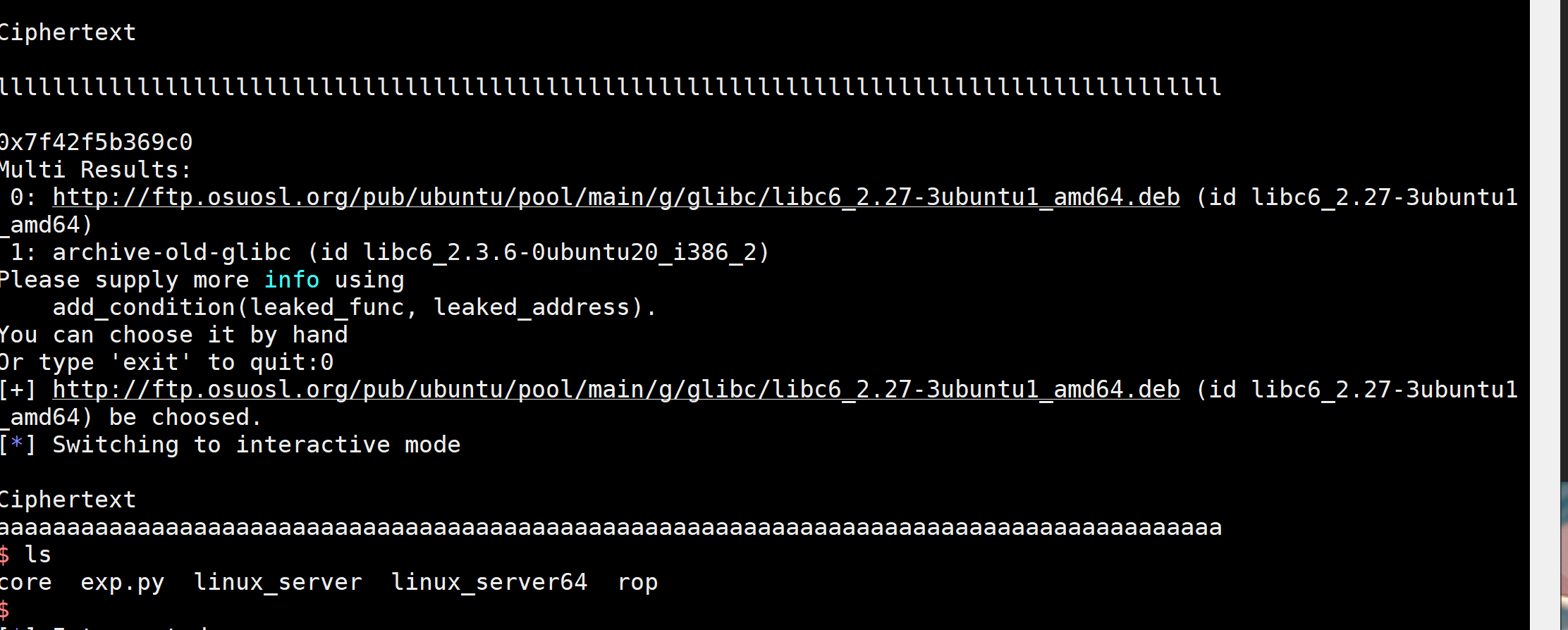
ciscn_2019_n_1
gets溢出后修改对应的浮点数即可
1 | |
ogeek babyrop
1 | |
get_started_3dsctf_2016
打法很多
ropchain是第一想法
后来看到了后门也可以利用
1 | |
1 | |
远程环境有毛病只能shellcode了
cgctf note
有些地方还是没有完全搞懂
大致攻击流程复现了下
unsorted bin leak
首先分配大小超过0x80的堆块free后show来leak//因为程序没有检查show时分配的堆块还是否存在
调试发现leak地址位于main_arena+88处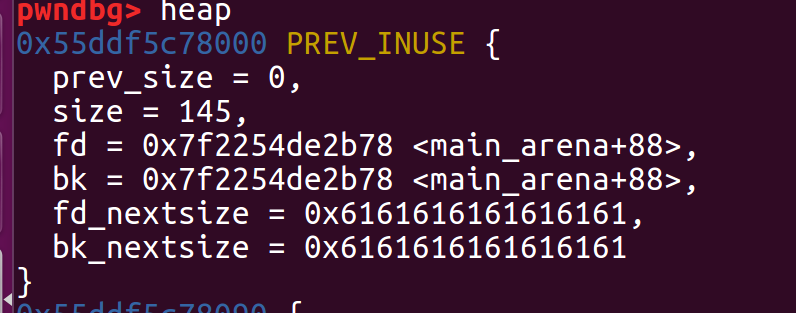
libc_base就是leak地址-(main_arena+88)
fastbin attack
通过修改fd指针指向malloc_hook
再edit到onegadget处调用一次malloc即可
脚本如下
1 | |
hctf2016–fheap
简单的UAF
分析出程序的结构体后发现free后未置0
利用uaf可以先分配三个小堆块然后分配0x20正好能覆盖到结构体中的指针
因为开启了pie通过覆盖低位为puts函数
下面就能调用delete函数leak出libc
然后整出system地址后重复一次攻击即可
1 | |